Pratiques et Techniques en Plaisance  | Imprimer |  Fermer la fenêtre

LE POINT ESTIMÉ

Présentation

• Le pilotage et l’estime, sans moyen astronomique, les premiers navigateurs n’avaient que cela pour caler leur route. Pas de moyens objectifs et précis pour évaluer leur vitesse, pas de carte indiquant la présence de la terre, et au large aucun élément situant la position du navire.

Il a fallu classer l’art de la navigation dans les sciences mathématiques, pour trouver des solutions sortant de l’espace limités de leurs certitudes. Et recadrer de faux problèmes de pilotage : des îles fictives, des vigies inutiles, abondamment semées (écueils qu’on croyait avoir aperçu en haute mer et qu’on signalait sans avoir pris la peine d’en vérifier l’existence). Des lignes côte subjectives et erronées. Tout ceci provoquant au pire du sang et des larmes, au mieux des retards coûteux et dangereux : pour sécuriser un atterrage, on sondait beaucoup, voire mettre à la cape, sans parler des allongements de routes inutiles
Avec cette manière d’obtenir les éléments de l’estime, les erreurs sur la dérive, l’ignorance des courants, les faibles vitesses et les durées des traversées, les vents variables, l’abus des calculs graphiques, on trouvera naturelles les énormes erreurs que l’on rencontre dans la position estimée du navire.

Pour lire ce dossier, dans sa version initiale (mise en page de 1931), télécharger le PDF de ce chapitre à ce lien

Le fac-similé dans la version de 1931, est ici

---

I. - Les éléments et le calcul de l’estime.

Jusqu’à la fin du XVIIIe siècle la presque totalité des grands voyages se fit avec les seuls procédés de l’estime, dont les résultats étaient partiellement rectifiés par l’observation de la latitude.

Pour faire le point estimé il fallait déterminer ses éléments, c’est-à-dire la vitesse du navire et la direction de la route ; puis trouver le moyen de les utiliser pour conclure le point, autrement dit résoudre le problème loxodromique. Or, dans ces trois parties, le progrès a été très lent. Voyons d’abord la vitesse. On peut dire que pendant tout le XVIe siècle elle a été appréciée simplement à vue, sans le secours d’aucun instrument de mesure ; même pas du loch devenu plus tard si courant.
La description de ce dernier apparaît pour la première fois en Angleterre dans un livre de Williarn Bourne intitulé A regiment for the sea, publié en 1577, et il faut aller en 1607 pour en trouver une nouvelle mention dans un Voyage aux Indes Orientales publié par Purchas. Puis après 1620 environ, on le trouve dans tous les traités de navigation par exemple chez Gunter en 1623, Snellius en 1624. Métius en 1631, etc., Fournier en 1643. Ce dernier dit alors, le décrivant : « depuis quelques années les Anglais attachent à une ligne nouée une petite palette de chêne d’environ un pied (30 cm.) sur cinq ou six pouces de large (12 à 15 cm.), chargée sur l’arrière d’une petite bande de plomb, avec aux côtés deux petits tuyaux de bois pour la soutenir mieux. » Cependant la machine ne s’imposait pas puisque, entre autres, vers 1633 on n’en connaissait pas l’usage dans la marine espagnole où Porter, qui en parla à cette époque, mettait en doute son importance et puisqu’en 1673 encore il ne figure pas dans le Arte de Navegar publié à cette date à La Havane par Don Lazaro de Flores. Porter lui préférait la connaissance pratique que chaque pilote doit avoir de la marche de son navire dans les diverses circonstances où il se trouve. Et on rencontre des idées analogues en 1637 dans le Seaman’s Practice de Norwood et plus tard chez le P. Fournier, qui les rapportent il est vrai pour les combattre, mais précisément parce qu’elles étaient courantes. On s’y tenait cependant encore beaucoup plus tard comme en témoigne ce passage extrait de l’Abrégé de Pilotage de Coubard et Lemonnier, édité en 1766 :« On fait ordinairement l’estime, y est-il dit, à voir passer l’eau le long du bord du vaisseau, ayant égard à la bonté du vaisseau, la force du vent, à la manière dont il enfle les voiles, si l’on va au plus près ou non, la dérive, qui pourrait faire juger que l’eau va plus vite qu’elle ne fait effectivement, à la marée et aux courants, si le vaisseau est lesté, nouvellement suifvé, etc. »

• D’autres machines que le loch d’ailleurs étaient décrites.
  • Divers ouvrages parlent de la roue, déjà connue de Vitruve, que l’on trempait dans l’eau le long du navire et dont on comptait le nombre de tours au moyen d’engrenages qui faisaient tomber de temps en temps un caillou dans un bassin.
  • Barthelemi Crescentius, vers 1607, avait aussi proposé une singulière machine faite d’une sorte de roue d’anémomètre formée de deux planchettes de bois rectangulaires, qui enroulait autour de son axe, en tournant sous l’impulsion du vent relatif, une longue ficelle dont la longueur enroulée devait permettre le calcul de la distance parcourue.
  • Norwood enfin indique un dernier procédé, perfectionné et repris de nos jours en Angleterre ainsi que l’atteste le dernier Manuel de Navigation de l’Amirauté de ce pays. Il consistait à mesurer la vitesse en faisant deux marques sur le bâtiment et en comptant le temps qu’une certaine masse d’eau mettait à aller de l’une à l’autre. Norwood fait d’ailleurs remarquer les imperfections de la méthode dues à l’entraînement de l’eau le long du bord, entraînement qu’il appelle le phénomène de l’eau morte, et à la difficulté d’appréciation très exacte du temps.

Il ne suffisait pas enfin d’avoir un instrument de mesure, il fallait encore savoir ce que l’on mesurait, rapporté aux dimensions de la Terre ; connaitre la longueur de la minute du grand cercle de la Terre, faute de quoi la distance parcourue ne pouvait pas être transformée en coordonnées géographiques.
C’était ainsi la question de la mesure de la Terre qui se posait. C’est donc le moment de parler des deux opérations suivantes qui furent entreprises pour fixer la valeur du rayon ou du degré terrestre.

• La première est due à Wright, dont nous aurons longuement à parler à propos de la carte marine. Il la décrit dans un célèbre ouvrage : Certain Errors in Navigation detected and corrected, paru pour la première fois en 1599. Wright fait remarquer qu’on a besoin de connaître le rayon de la Terre pour pouvoir calculer la dépression de l’horizon, élément qui intervient dans toute hauteur prise par rapport à l’horizon de la mer et c’est dans ce but qu’il dit entreprendre sa mesure.
  Il la fit en l589 à l’entrée de Plymouth sur le mont Edgecombe, devant l’église Maker, au moyen d’un instrument en forme de triangle rectangle dont les côtés de l’angle droit avaient environ 3 pieds (91cm,5) de longueur et dont il divisa l’un d’eux en 10.000 parties égales ; ce qui, au moyen d’une table des tangentes, lui donnait l’angle au sommet opposé. Il choisit deux stations distantes de 202m,4, la plus longue distance que le terrain lui permettait de prendre ; et de la visée d’un petit rocher : Shagstone rock et de l’horizon il conclut la distance du rocher (5.433 m. au lieu de 5.260 environ), l’altitude et le rayon cherché. Il ne tint pas compte de la réfraction et conclut, et encore grâce à une compensation d’erreurs, pour le rayon à la valeur de 5.580 km., trop faible de 800 km. à peu près. Par malheur cette valeur de 5.580 km. donnait au mille une longueur de 1.620 m. que l’on jugea assez voisine de la longueur admise alors par les pilotes pour permettre de trouver dans l’opération une confirmation de cette dernière valeur, laquelle se trouva ainsi appuyée sur l’autorité de Wright, qui fut très grande.
  Wright avait aussi indiqué une méthode plus sûre de faire la mesure en question. Elle consistait dans la mesure d’un arc de méridien corrélativement avec celles des latitudes des extrémités ;
• et son compatriote Norwood, qui avait commencé par être marin avant de devenir professeur de mathématiques, la mit en pratique ; d’autant que, d’après Wright toujours, la mesure du rayon de la Terre devait encore servir à faire dépendre les unités des mesures communes de la longueur du degré et non pas, comme on le faisait, de la longueur d’un grain d’orge, puisqu’on définissait le doigt par trois grains d’orge mis bout à bout.
  • Donc en 1633 et 1635 il mesura la latitude du milieu de la ville d’York et celle de Londres près de la Tour, et cela le 12 juin, c’est-a-dire au solstice d’été. Il trouva 2°28’ de différence entre les latitudes, ce qui peut être exact ; puis il fit une entreprise peu ordinaire, qui consista à mesurer directement à la chaine la distance entre les deux villes, éloignées de 275 kilomètres. Sa chaîne avait une trentaine de mètres. A la vérité il dit que parfois il se contenta de compter le nombre de ses pas, après avoir acquis, remarque-t-il, assez de pratique pour approcher très près de la vérité. Il tint compte bien entendu des directions dans lesquelles il mesurait au moyen d’un graphomètre et même des pentes de la route. Bref il attribua une différence de longitude de 1°2’3" aux deux points, quantité légèrement trop forte et 9.149 chaines à la distance entre leurs parallèles. Cela faisait 367.200 pieds au degré, alors qu’on n’en comptait, dit-il, que 300.000. Le mille valait donc d’après sa mesure 1.866m,6, ce qui constituait une approximation d’autant plus remarquable qu’il affirme n’avoir mis que 10 à 11 jours à la mesure itinéraire.
  • En conséquence il proposait de donner au nœud 51 pieds, ou 50 seulement pour tenir compte de l’entrainement de la ligne de loch, au lieu de s’en tenir comme on le faisait à 42 pieds, soit à 1540 mètres à peu près pour la minute. Car telles étaient alors les erreurs de la graduation de la ligne de loch.
  • On va voir comment fut reçue la suggestion de Norwood. Elle rencontra en effet de longues résistances que lui-même attribue à différentes causes.
    • En premier lieu, en faisant le nœud trop court, les marins prétendaient corriger l’imperfection des cartes plates où les degrés de longitude ont partout la même valeur au lieu d’aller en diminuant quand on se rapproche des pôles ;
    • Puis ils demandaient quelle était la véritable valeur ;
    • Enfin ils disaient qu’avec leur pratique le point qu’ils calculaient en comptant un trop grand nombre de nœuds, les mettait en avant de leur position exacte et qu’ils assuraient ainsi la sécurité de leurs atterrissages. « En toute estime, disait encore le P. Fournier, il vaut mieux se faire plus de l’avant que de derrière…, car il vaut mieux être 20 lieues de l’arrière (du lieu ou on se croit) que d’une seule portée de canon trop tost de l’avant. »

Si maintenant nous franchissons un siècle, nous serons préparés à ce que nous allons constater.

• En 1727, Radouay, capitaine des vaisseaux du roi, qui annonce, dans ses Remarques sur la Navigation, les officiers savants de la fin du siècle, fait en effet, à l’égard de la graduation de la ligne de loch, des révélations étonnantes. Le nœud de la ligne de loch des pilotes, assure-t-il, est trop petit. Ils le comptent de 41 pieds 8 pouces (13m,34), alors qu’il devrait être de 47 pieds 6 pouces (15m,20), d’après les mesures des académiciens faites en 1672, – il s’agit de la mesure de Picard, qui permit à Newton de vérifier la loi de la gravitation, – car elles ont donné 17.118 pieds (5.457 mètres) pour la lieue. Le nœud était donc de 1/8è trop court, ce qui augmentait d’autant, en apparence, la vitesse du navire, puisqu’on en comptait plus qu’on n’aurait dû le faire.
• Signalée cette fois par rapport à une mesure certaine, l’opération de Picard étant, d’après Faye, la véritable origine de la géodésie et ayant toujours été considérée comme telle, on pensera que cette erreur si grossière a été corrigée aussitôt signalée. Mais il n’en est rien. Chabert, un des premiers officiers astronomes, dans la relation du voyage en Acadie, qu’il entreprit en 1750 et 51, pour corriger les positions géographiques de cette région, porte les mêmes plaintes : « Quantité de pilotes, dit-il, donnent encore 41 pieds 8 pouces au nœud, au lieu de 47 pieds 7 pouces, mesure que le ministre Maurepas a pourtant prescrit d’adopter. Il n’y a point d’officier qui ne s’en plaigne, mais inutilement. »
• Bouguer, fils de professeur d’hydrographie et professeur lui-même, au Croisic, puis au Havre, se plaignait aussi dans le même sens en 1747, dans un mémoire à l’Académie, dans lequel il signale que « la plupart des pilotes comptaient le nœud la 1/120e partie de l’ancien mille, comme le disait Radouay en 1725 ». Et cette question le préoccupait depuis longtemps, puisque dans le récit de son voyage à l’équateur il écrivait qu’il fallait déterminer la forme du méridien pour savoir si les marins devaient donner au mille la même longueur à toutes les latitudes : inquiétude excessive.
• Enfin, en 1781 encore, la graduation exacte n’était pas fixée. Gaigneur, autre hydrographe, dans son Pilote instruit, publié à Nantes, à cette date, écrit en effet que « la majorité des navigateurs s’écarte de la division absolue de la ligne de loch, qui doit être de 47 pieds 6 pouces entre chaque nœud ; que chacun la modifie selon les préjugés, les uns ne donnant que 42 pieds 6 pouces, d’autres que 43, 44 ou 45 pieds (14m,62 comme aujourd’hui), cette dernière valeur étant autorisée du sentiment de Verdun de la Crène, Pingré, Borda » ; car il était nécessaire de diminuer un peu la longueur exacte pour tenir compte de l’entrainement du flotteur par le bâtiment.

Il est vrai que les pilotes essayaient de corriger les erreurs de la graduation du loch par une autre erreur commise, cette fois, dans le sablier qui l’accompagnait. Le nœud est la 120e partie du mille, et le sablier qui sert à les compter est de 30 secondes : 120e partie de l’heure ; de sorte que le nombre de nœuds filés en 30 secondes est le même que le nombre de milles ou de minutes d’arc de grand cercle, parcourus en une heure. En employant des sables de 30 secondes, avec des divisions de la ligne de loch trop courtes, les pilotes estimaient la vitesse trop grande. Mais si le sable n’était plus que de 25 ou 26 secondes, l’erreur se trouvait en partie rectifiée. C’est ce qui avait lieu souvent, les sabliers étant généralement trop courts ; peut-être, par suite de l’usure des grains produite à la longue par leur écoulement, surtout si ces grains provenaient de coquilles d’œufs pilées. Mais, dit encore Chabert, « c’étaient là de mauvaises pratiques ». Le sablier n’était pas toujours trop court du reste.

• Le Gentil, pendant ses voyages dans la mer des Indes, où il manqua les deux passages de Venus sur le Soleil, de 1761 et 1769, eut un jour, étant à la mer, l’idée de vérifier le sablier. Pour cela, il prit des hauteurs de Soleil voisines, en comptant l’intervalle de temps qui les séparait avec le sablier à vérifier. Les hauteurs lui donnant les angles horaires correspondants et par suite le temps écoulé entre les observations, il trouva pour durée de l’écoulement du sable 34",25, valeur qu’il vérifia à terre, et qu’il trouva exacte.
• Aussi Gaigneur recommande-t-il de vérifier le sable au moyen du pendule qui bat la demi-seconde. On devait faire ce pendule en fil de soie, avec balle de plomb de 3 à 4 lignes (6,7 à 9 millimètres) de diamètre ; le fil serré à une fente. Sa longueur, jusqu’au centre de la balle, devait être de 9 pouces, 2 lignes, 1/7e (24cm,8) et on devait écarter initialement la balle de sa position d’équilibre de 3 à 4 pouces (8 à 11 centimètres).
• Enfin, quelquefois, les pilotes pensaient ne pas commettre d’erreur malgré leurs instruments défectueux, en aidant plus ou moins la ligne de loch à se dévider, « ils ne jetaient pas tous le loch de la même manière ». En résumé, le loch, déjà si imparfait par essence, ne pouvait, avec ces pratiques, donner des résultats satisfaisants.

Le compas valait-il mieux ? Il faut distinguer entre le compas de route avec lequel on gouvernait, et le compas de variation qui servait à l’observation des azimuts, d’où on concluait la valeur de l’angle de l’aiguille et du méridien. Ils avaient l’un et l’autre des roses à aiguille simple, de formes variées. Même on en avait essayé de forme circulaire, en anneau. Ordinairement, l’aiguille était un losange très allongé et la rose était collée dessus ; un petit cône creux de cuivre ou de laiton servait de chape, de chapelle comme on disait au XVIIe siècle, et le pivot était fait d’une tige très fine, trop fine, d’acier. Pivot et chapelle pouvaient aussi être d’airain. Radouay se plaint beaucoup des défauts de leur construction. A la longue, les roses s’affaissaient vers l’est et vers l’ouest, ou elles n’étaient pas soutenues ; car on ne les soutenait pas toujours par une circonférence de talc (mica) collée par dessous. Pour y remédier, on avait essayé des aiguilles en forme de large losange réduit à ses côtés ; mais alors leur axe magnétique n’était pas fixe.
D’autre part, la rose était enfermée dans une boite, d’abord en bois, qui était suspendue à la cardan à l’intérieur d’une autre, plus grande. Les planches jouaient, et aux grands roulis, la boite intérieure venait buter contre l’extérieure.

• Plug tard, on fit généralement la boite intérieure en laiton ou en cuivre. Les compas de route étaient enfermés dans l’habitacle. Au XVIIIe siècle, c’était une petite armoire fixée sur le pont, vers le mât d’artimon, de manière à ce qu’on pût voir commodément au dedans. Elle était divisée en trois compartiments, celui du milieu étant destiné à loger une lampe et les autres des boussoles. Au-dessus de ces instruments, on déposait les montres et les sabliers. Enfin elle était installée dans le sens de la largeur du bâtiment, de telle sorte que l’homme de barre avait toujours un compas sous les yeux, de quelque bord qu’il se trouvât place.
• Antérieurement il n’en était pas tout à fait de même : « Habitacle ou gesole, lit-on dans le P. Fournier, sont trois niches ou armoires qui sont au pied du mât d’artimon : en l’une est la lumière, en l’autre la boussole, en la troisième le poudrier ou horloge. »
  • Cet habitacle était une cause d’erreur. En 1750 Chabert croyait nécessaire de vérifier s’il était fixé de manière que ses cotés fussent parallèles à la quille ; car sa position déterminait celle des boites carrées des boussoles qui y étaient introduites ; et il y avait souvent des inégalités attribuables à cette négligence.
• Les imperfections de toutes sortes dans la confection des boussoles étaient donc cause de nombreuses irrégularités. Colomb remarquait déjà que les aiguilles de différentes trempe et construction n’offraient pas les mêmes angles de variation. Barentz à la Nouvelle Zemble attribue une erreur grossière qu’il commit à la variation de l’aiguille de la boussole qui était enfermée dans une boite garnie de fer ; et sur onze vaisseaux hollandais allant en 1623 aux Indes Orientales par le sud de l’Amérique, on remarque que les boussoles différaient beaucoup les unes des autres. Et on voit aussi que les progrès étaient très lents.
  • Dans les Mémoires de l’Académie des Sciences de 1686, on fait remarquer que l’aiguille déclinait tout autrement dans une boite de cuivre ou dans une boite de bois. En 1716, on formule de nouveau la même plainte ; les boites en laiton sont sujettes à erreur parce que ce métal contient des granules de fer. Aussi La Hire propose-t-il des boites de marbre. On ajoute que « les boussoles dont on se sert sur mer sont si grossières qu’on ne peut assez s’étonner comment on s’y fie pour la conduite d’un vaisseau ». Il est vrai « qu’on n’a rien de meilleur, ni de plus commode »
  • Dans les Mémoires de l’Académie de Marine aussi, on s’inquiète de toutes ces imperfections. En 1769, on commença à s’occuper de la boussole dans cette savante assemblée, en faisant remarquer que le laiton des boîtes produisait des dérangements. En 1771, année où l’Académie de Marine est affiliée à l’Académie des Sciences « afin d’accélérer les progrès des sciences nautiques », Mannevillette, jusqu’à son époque le plus grand hydrographe de tous les temps et de tous les lieux, écrit d’Hennebont que Retail, qui construisait depuis vingt ans des boussoles pour la Compagnie des Indes, n’emploie que le cuivre rouge à l’exclusion du laiton. Il fait observer aussi qu’on ne doit pas mettre deux compas dans l’habitacle, comme on le faisait ordinairement pour diminuer les chances d’avoir une aiguille « dormante », leur différence pouvant aller à 5 ou 6°, comme il l’avait expérimenté en 1767, par suite de l’action réciproque des aiguilles l’une sur l’autre. Ces remarques avaient déjà été faites plus de trente ans auparavant par Duhamel et Morogues, de l’Académie des Sciences.
  • Fleurieu, en 1775, expliqua que ces actions réciproques devaient se produire, puisque la sphère d’action des aiguilles s’étendait à 12 pieds (4 mètres) « quoique enfermées dans une boîte et sous glace ». Il se plaignait également de l’habitude qu’on avait de placer des fanaux à proximité des compas et de ne pas les éloigner assez des canons.
  • Enfin, on trouve encore, pour préciser ces faits, des expériences rapportées en 1779, par de Gaulle. Il dit que dans les petits navires du roi, les deux roses de l’habitacle, séparées par le compartiment du milieu, réservé à la lumière, sont éloignées de 15 à 18 pouces (40 à 48 centimètres), même de 12 à 13 (32 à 35 centimètres) seulement quelquefois ; et que, dans ces conditions, avec des aiguilles de 6 pouces 9 lignes (18 centimètres) de long et de 4 lignes (9 millimètres) de large, et chape d’agate, les inégalités atteignent 26°.
  • L’Académie de Marine avait également ordonné à ce sujet des expériences qui furent concluantes et elle en répandit dans les ports les résultats qui furent tirés à 900 exemplaires.
     
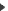
    Faut-il s’étonner après ces constatations que la déclinaison même ait pu longtemps être niée par quelques-uns ? « Des mariniers sont si ignorants qu’ils sont persuadés que leur aiguille regarde toujours le Nord », écrivait le P. Fournier. Or ils n’étaient pas les seuls à nier ou à avoir nié la déclinaison. D’après Navarette, Fernandez de Enciso serait l’auteur, en 1519, du premier traité systématique de navigation, destiné à remplacer les indications données sur les cartes. Cet ouvrage semble avoir été peu connu.

Au contraire le Arte de Navegar du mathématicien Medina, paru à Valladoïd en 1545, a été très répandu. Et Medina nia l’existence de la déclinaison ; il n’a pu concevoir que le méridien magnétique et le méridien géographique aient pu être choses différentes ! Il avait du reste dans cette affirmation des circonstances très atténuantes. Elles sont – et sans remonter au temps où la « calamite » sans pivot flottait simplement sur un fétu à peu près encore comme dans quelques boussoles chinoises récentes – dans l’imperfection des instruments, dans la grossièreté des observations, enfin dans le fait qu’à son époque la déclinaison avait une faible valeur sur les côtes occidentales de l’Europe méridionale.On observait cette déclinaison à terre par « l’ombre du Soleil en son midi » ou par deux observations du Soleil faites en deux temps également distants du midi ; en mer par les amplitudes ortives ou occases, aux levers et couchers du Soleil, ou par l’observation de la Polaire, quand elle était au méridien ; ce dont il était facile de s’assurer par des alignements.

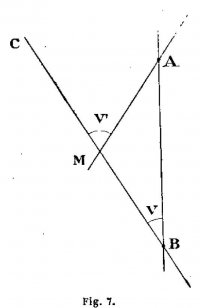
Par exemple au milieu du XVIIIe siècle cela avait lieu quand l’Étoile était juste au-dessus ou au-dessous de la poitrine de « Cassiopée ». Et nous avons vu qu’on obtenait des résultats des plus variés. On mettait encore les inégalités sur le compte de la faiblesse ou du vieillissement des aiguilles et en 1586 Ricbard Polter déclarait que des aiguilles touchées avec des pierres d’aimant différentes avaient des déclinaisons différentes. Enfin on cherchait à réaliser des aiguilles parfaites ne déclinant point. Crescentius, en 1607, annonça qu’une aiguille en forme de V peu ouvert ne décline point (fig. 1). Il précisa que les deux pointes devaient être distantes de 22°30’. D’autres attribuèrent la même propriété à des aimants sphériques ou cylindriques que l’on faisait flotter, ces derniers verticalement ; ils affirmaient que ces corps aimantés gardaient une orientation fixe, la ligne de leur pôles marquant précisément le méridien. Cortes en 1556, rival heureux de Médina, dans son Breve Compendio de la sphera y de la arte de navégar croit à la déclinaison ; mais il suppose que l’aiguille se dirige toujours vers un même point du ciel, idée qui avait été celle de Colomb et que Cardan accepta en déclarant que l’aiguille se dirige constamment sur l’étoile Polaire, « chose impertinente et ridicule », dit le P. Fournier. Paracelse d’ailleurs était de la même école et plaçait ce point dans la Grande Ourse. Cependant nous nous garderons de jeter la pierre aux auteurs de ces idées étranges pour nous. Pour les juger, nous ne devons pas oublier que nous savons, alors qu’ils cherchaient et précisément pour nous apprendre ce que nous savons. Mis nous-même en présence d’un domaine nouveau de la nature, à définir et à expliquer, nous opérons comme eux, imaginant tout le possible que nous éprouvons par l’expérience et la réflexion et c’est ainsi que nous avançons peu à peu dans la conquête du vrai.

Le compas de variation ne différait pas sensiblement du compas de route, seulement il portait deux pinnules diamétralement opposées, fixées sur le bord de la boite extérieure, et au dessus de la rose, un fil tendu perpendiculairement à la direction des pinnules et fixé à la même boite par ses extrémités. Il y avait aussi un fil tendu d’une pinnule à l’autre.
La figure 2 le représente d’après un modèle du XVIe siècle. Pour relever le soleil, on transportait le compas dans un endroit du bâtiment d’où l’astre pouvait être commodément aperçu. On avait soin de l’installer sur un corps mou, « par exemple sur un capot ou une redingote » suivant la recommandation de Gaigneur, afin de pouvoir le caler et l’orienter aisément ; car il fallait tourner la boite toute entière pour viser dans une direction avec les pinnules : et, pendant qu’un observateur faisait cette visée, un aide, nécessaire, lisait la graduation qui tombait sous le fil perpendiculaire. Ce moyen était compliqué et pouvait donner lieu à de multiples erreurs. Aussi n’est-on pas surpris de voir dans Radouay que le compas de variation et le compas de route différaient souvent de 10°, et Gaigneur conseiller de comparer les deux compas car « ils diffèrent souvent ». Il est surprenant de voir les choses demeurer en cet état jusqu’à une date avancée dans le XIXe siècle. En Angleterre, Robertson, dans son cours de Mathématiques à l’usage des marins, décrit le même compas de variation en 1780. En France, le Vade-Mecum du Marin, de Guépratte, qui fut en beaucoup de mains, porte encore, dans une édition postérieure à 1835, que le « compas de variation contient deux pinnules opposées » et « qu’il peut se transporter facilement d’un lieu à un autre ». Ainsi, à ce moment, on n’avait pas adopté, moyen si commode, l’alidade centrée sur le centre de la rose, alidade pourtant proposée par Ed. Wright dès la fin du XVIe siècle. Il en était d’ailleurs généralement de même encore en 1870 puisqu’à cette date, le Cours de Navigation de Dubois ne montre qu’un compas de relèvement portant deux pinnules liées au couvercle même de la rose. Aucune alidade mobile et ne faisant pas partie du compas n’est figurée. Et Dubois écrit que ce compas peut parfois se transporter, étant monté à cet effet sur un trépied. Peut-être que la pratique du déplacement se maintenait parce que sur les bâtiments à voiles, le gréement pouvait masquer une grande étendue du champ de vision.

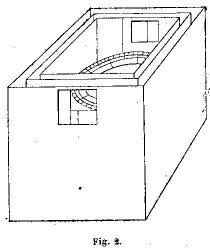
Cependant l’alidade est figurée et décrite dans la 4e édition du traité de Caillet qui date de 1868, et l’auteur ajoute que depuis quelque temps et à l’imitation du Standard Compass de la Marine anglaise, « l’usage se répand à bord des navires d’installer un compas de relèvement à poste fixe ». Ce compas, dit-il, a quatre aiguilles parallèles de 18 à 20 centimètres symétriquement placées par rapport la ligne médiane. A cette époque où en Angleterre on se préoccupait activement des déviations du compas, il devenait évidemment nécessaire d’installer celui-ci à un poste fixe et de ne pas toucher à l’orientation de l’habitacle qui devait contenir les correcteurs. Une alidade centrée sur le centre de la rose avait pourtant été re-proposée par Fleurieu mais avec des complications d’installation, et, en fait, on se servait tout au plus du compas azimutal décrit par Pézenas, par exemple, en 1766, dans son Astronomie des Marins et en 1814 dans l’édition de Rossel, du Cours de Navigation que Bezout avait fait autrefois, à partir de 1765 environ, aux gardes-marines. Ce compas azimutal était un compas de variation auquel on ajoutait, recouvrant la glace, un cercle de bois ou de cuivre, qui portait, non pas en son centre, mais en un point de sa circonférence, une équerre verticale pivotant autour de ce point et servant ainsi d’alidade. Seulement cette équerre ne pouvant mesurer commodément que des angles de 45° de part et d’autre du diamètre de la rose passant par le pivot de l’équerre, ce pivot pouvait occuper quatre positions différentes sur la boite du compas, à 90° les unes des autres. Enfin, les pilotes à qui on laissait le soin de la route, ne relevant guère le Soleil qu’à son lever ou à son coucher, il arrivait, dit Radouay, qu’en hiver, dans l’Atlantique nord, on restait souvent plusieurs jours sans avoir de variation. La figure 3 montre ce compas d’après un original de Seller dans une édition de 1740. Pour relever le Soleil on mettait le fil entre le Soleil et le bras vertical de manière à recevoir l’ombre du fil sur les deux côtés de l’équerre. On mettait donc le sommet de l’équerre, le matin, sur le point W.

 
Les éléments de l’estime déterminés, bien ou mal, il fallait en tirer parti, trouver le point d’arrivée, connaissant le chemin parcouru, la direction et le point de départ.
Cela revenait à résoudre le problème de la loxodromie ; problème difficile, qui, avec celui de la longitude par les méthodes astronomiques a été une des pierres d’achoppement de la science de la navigation pendant de très longues années. Et ceci nous conduit à l’examen des cartes dont se servaient les navigateurs, d’autant plus directement qu’il n’y a aucun doute que les cartes aient été voulues non pas seulement pour y figurer le dessin des côtes, mais encore et surtout, au moins dans le cas de la carte de Mercator, pour donner une solution graphique des problèmes de l’estime. C’est ce qu’on n’a pas suffisamment remarqué, semble-t-il, en ne considérant les cartes que d’après leur valeur géographique, alors que véritables nomogrammes, elles étaient plutôt un instrument de calcul. Le nom de carte « réduite » donnée à la carte de Mercator nous paraît confirmer cette opinion. En rapprochant le mot « réduite » du mot « réduction » dans « Quartier de réduction », on comprend que la carte marine n’ait été avant tout qu’une carte pour calculer des routes « réduites »

On a quelque peine à se faire une idée précise de ce qu’étaient les premières cartes des navigateurs, tout simplement parce que l’imprécision de leur construction était une de leurs caractéristiques. Tous les auteurs s’accordent à déclarer que c’est grâce au prince Henri de Portugal que les navigateurs ont pris l’habitude de l’usage des cartes, que c’est lui qui a commencé à les faire établir. Ces premières cartes marines furent du reste construites par des voies différentes. Il y avait les cartes plates ou cartes communes où l’on supposait ou croyait supposer la Terre plate dans l’étendue de la carte. Elles comportaient un canevas formé de parallèles et de méridiens rectilignes équidistants, avec « quantité d’échelles », chaque parallèle « en ayant une particulière ». Bouguer dit en 1753 qu’elles sont encore employées malgré leurs imperfections, que tout le mode aperçoit sans peine. On y représentait les loxodromies par des droites. Or, le rapport de la largeur à la hauteur d’une région y est altéré, et également le calcul par la carte des différences de longitudes ; la carte ne conserve pas les angles et ne permet pas de trouver les directions des routes, d’où les marins accusaient leurs compas et les courants ; elle ne conserve pas les distances. Puis on en trouvait qui étaient faites par « routes et hauteurs » c’est-à-dire par directions et parallèles de latitudes, ces derniers étant seuls tracés à l’exception des méridiens. « Ceux qui naviguent par route (direction) et hauteur (latitude), s’ils sont assurés de l’un et de l’autre, ils seront aussi assurés de leur longitude », disait-on. Elles comportaient une seule échelle.

D’autres étaient tracées par « routes et distances ». C’était des cartes itinéraires sur lesquelles ne figurait aucun canevas. « Il est impossible de s’en servir sur l’océan pour de grands voyages, disait le P. Fournier, parce qu’il est impossible que beaucoup de distances s’accordent entre elles ».

Ces dernières cartes, en effet, n’étaient pas définies. Elles dépendaient du chemin suivi pour aller d’un point à un autre Soit à placer le point B en partant de A (fig. 4). Si on va de A en B par le parallèle AH et le méridien HB on tracera B sur une perpendiculaire à la droite qui représentera AH, à la distance BH de H et on aura une carte plate. Si on va maintenant en B par le chemin AEB, on portera AE = HB sur la perpendiculaire en A à la représentation de AH ; puis EB sur une droite parallèle à AH menée par E et on trouvera une nouvelle position B1 pour le point B. Les méridiens obtenus en joignant de tels points B1 seront sur une sinusoïde puisque, AN étant sur l’équateur on a EB = AH cos φ, φ étant la latitude. On obtiendra ainsi la carte sinusoïdale de Jehan Cossin, où les méridiens sont de telles sinusoïdes. En troisième lieu, si l’on va de A en B en suivant la loxodromie AB et portant B par la distance parcourue sur une droite de même azimut en A que la loxodromie AB, on trouvera un troisième point B2 pour représenter ce même point B. Toutefois les points B, B1, B2 ont même latitude. Mais ce qui précède montre qu’on est loin de pouvoir prétendre, comme on l’a dit quelquefois, que de telles cartes étaient en réalité des cartes de Mercator, que les anciens géographes ou marins construisaient sans s’en douter. Enfin ces cartes par « routes » étaient couvertes de roses des vents « peintes ».

Dans tout cela le problème loxodromique n’était pas vraiment abordé. Il fallait d’abord étudier la courbe en elle-même. Le véritable initiateur fut ici Pedro Nunes, professeur de mathématiques à Coïmbre. Il commença à s’en occuper avant 1537, année où parut de lui son premier ouvrage, écrit en portugais, lequel fut réédité en latin et augmenté en 1566, sous le titre : Arte et Ratione Navigandi. Or nous verrons que la question de la loxodromie ne fut complètement résolue qu’en 1695. A l’époque de Nunes, le calcul infinitésimal n’étant pas né, à beaucoup près, la loxodromie offrait des difficultés proprement insurmontables. Nunes pensa donc à la construire approximativement. Il y parvint de la manière suivante.

En A (fig. 5) situé sur l’équateur de la Terre supposée sphérique traçons un arc de grand cercle AR’B faisant avec le méridien un angle donné A. Le long de cet arc AB l’angle A : azimut orthodromique, varie constamment. Soit B le point ou cet angle est devenu A + ΔA ; ΔA étant petit. Au point B on trace alors un second arc de grand cercle BC faisant avec le méridien de B un angle A, avec celui de C un angle A + ΔA. On fait de même en C pour tracer l’arc CD, etc. Nunes remplaçait ainsi, par des constructions faciles, la loxodromie par une série de points B, C, D... qui en étaient voisins. Cependant il ne pouvait pas se rendre compte de la valeur de l’approximation. Il pouvait d’ailleurs trouver aisément par le calcul les coordonnées des points B, C, D… Mais nous pouvons depuis longtemps apprécier la construction de Nunes. On démontre alors que ces points B, C, D... se trouvent à très peu près sur une loxodromie d’azimut A + ½ ΔA. Tel était le point où Nunes, « le premier à avoir écrit des rumbs (loxodromies) », était parvenu.

Notons de suite que l’habitude de résoudre les problèmes de navigation géométriquement, sur un globe, était très répandue alors et qu’elle l’est restée très longtemps. L’ouvrage de Nunes contient l’exposé de telles constructions et les nombreux traités de navigation du XVIe et XVIIe siècle surtout font de même, généralement. On citait entre autres les globes construits par Gérard Mercator en 1541, ceux de Mullineux, de 1592 qui étaient plus grands que ceux de Mercator : et en 1594, dans un livre qui jouit d’une grande faveur, Robert Hues résolvait par le globe le problème de la détermination de la latitude par deux hauteurs de Soleil connaissant le temps entre les deux observations ; comme Nunes avait résolu le même problème de la latitude par deux hauteurs, la différence d’azimuts et la déclinaison du Soleil. Disons aussi qu’à la fin du XVIIIe siècle Robertson appelle encore « Globular Sailing » tout ce qui concerne l’estime et l’orthodromie. Les constructions directes sur un globe sont en effet aisées à comprendre et à concevoir et la méthode n’a que l’inconvénient d’être pratiquement inapplicable à cause des inexactitudes qui lui sont inhérentes par suite des dimensions nécessairement trop petites des globes que l’on peut employer. En effet sur un globe de 60 centimètres de rayon, déjà assez encombrant, le millimètre représente 11,5 milles.

 
Tel était l’état de la question après Nunes (ou Nonius) lorsque la célèbre « invention » de G. Mercator, qui eut lieu en 1555, si l’on en croit Navarette, aboutit à sa publication, en 1569, de la première « carte réduite » qui ait vu le jour. Il existe un exemplaire de cette carte à la « Nationale », et nous avons pu l’étudier. Or elle n’est pas correcte. Mercator lui-même a déclaré, d’après sa biographie, et à plusieurs reprises, qu’il ne savait pas exactement comment il fallait diviser le méridien de sa carte, et il comparait le problème qu’il avait cherché à résoudre à celui de la quadrature du cercle, auquel manquait toute démonstration. Il n’a de plus laissé aucune indication sur la manière dont il a opéré et nous en sommes réduits à des conjectures. Sur son globe de 1541 il avait tracé des loxodromies à peu près correctes, on ne sait comment ; sans doute à vue, ce qui est très aisé.

 
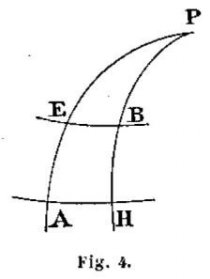
A-t-il employé en 1569 la méthode de Nunes, publiée en 1566 ? Ce qui suit permet au moins de poser la question. Il s’agissait pour la commodité de rectifier la loxodromie sur une carte à méridiens rectilignes et parallèles.

Construisons comme tout à l’heure les points BCD… sur un globe. Puis menons une ligne (en pointillé sur la figure) joignant ces points ABCD… Soit d’autre part sur la carte Q’Q l’équateur : mr, ns, ut… les images des méridiens équidistants MP, NP, UP… (fig. 6). Sur le globe la courbe pointillée ABCD… coupe le méridien MP en R. Pour porter le point r, image de R sur le méridien mr nous opérerons de la manière suivante. En a on tracera une droite arst… faisant avec le méridien de a l’azimut de la courbe pointillée ABCD… c’est-à-dire l’angle de AP et de AB (pointillée). Cet angle est différent de A ; il est plus grand. Nous avons dit que le calcul montre qu’il est voisin de A + ½ ΔA. Mais Mercator ne pouvait faire ce calcul. A défaut d’indications j’ai fait l’angle par, évidemment plus grand que A, égal à A + ΔA. Il y a là évidemment quelque arbitraire ; mais les points ABC sont très éloignés les uns des autres, le tracé ARB… (fig. 5) est donc incertain et d’autant plus, naturellement qu’un plus grand nombre de constructions aura été fait. Dès lors r étant obtenu on affectera au parallèle de ce point sur la carte la latitude de R relevée sur le globe. La cote de la latitude de R sera donc mr et ainsi de suite. On peut répéter la construction pour plusieurs valeurs de A et de ΔA. On pourra ainsi, par interpolation, tracer sur le canevas les parallèles de degrés ronds de latitude ou de 10 en 10°… On pourra encore chercher sur le globe le point d’intersection Y de la courbe pointillée AHB… avec un parallèle de latitude donnée, 20° par exemple, et placer l’image y de Y sur ars… par sa longitude relevée sur le globe ; ce qui donnera l’image du parallèle de 20°.

Et voici la vérification que l’on peut faire de la légitimité.de notre hypothèse : Reportons-nous d’abord aux documents. Dans sa Briefe Description of Universal Mappes and Cardes, imprimée d’abord en 1589, Blundeville donne les intervalles des parallèles de 10° en 10° sur la carte de 1569.
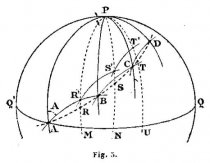
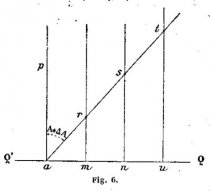
Nous avons pu consulter un exemplaire de Blundeville qui se trouve à la « Bodléienne ». Il y écrit que les trois premiers intervalles de 10° ne diffèrent pas de plus de 1° au maximum ; que de 30 à 40° il y a 11,5 degrés du premier intervalle ; de 40 à 50°, il y en a 13,75 ; puis 16,25 de 50 à 60°, 23,5 de 60 8 à70° ; enfin 36 de 70 à 80°. Or les intervalles exacts sont de 10°,05 ; 10°35 ; 11°1 ; 11°1 ; – 12°2 ; 14°2 ; 17°5 ; 24°0 ; 40°2 ; ou 12°2 correspond aux 11°5 de Blundeville, 14°2 à ses 13°75, etc. On voit que tous les intervalles donnés par Blundeville sont trop petits, de 1/30. De plus les différences avec les nombres exacts ne croissent pas régulièrement ; de sorte que ces nombres paraissent bien correspondre à des quantités résultant de relevés faits sur une figure géométrique et non pas calculés. C’est que la carte de Mercator, d’après ce qui précède, pourrait résulter de constructions approximatives faites sur un globe de 63 centimètres environ de diamètre. Je trouve en effet, en opérant comme il a été indiqué ci-dessus, qu’en faisant A = 30° et A + ΔA = 31° les différences entre les latitudes croissantes exactes et celles qui résultent des cotes relevées sur la carte d’une part (colonne 2) ; entre les latitudes croissantes exactes et celles de la courbe ABCD… (fig. 5) tracée par le procédé de Nonius (colonne 3) d’autre part, sont celles du tableau suivant :

Il semble que la comparaison de ces colonnes (2) et (3) emporte bien la conviction que Mercator a pu opérer par une voie très voisine de celle que nous supposons. Sa carte au total est, entre les parallèles de 60° sud et de 70° nord, trop courte de un quarantième environ, ou de 24 m/m sur 935 m/m. Quant à son développement dans le sens de l’équateur, il est égal à 1.974 m/m,5.

Enfin dans l’exemple choisi la différence entre les latitudes des points B, C, D… et les latitudes correspondantes des points de la loxodromie d’azimut 30°26’, qui sont de -4’ et de -3’ seulement pour les points B et E de latitudes 13°53’ et 23°48’ tombent à -1’ à l’extrémité du 15e arc et deviennent nulles à partir du 25e par 61°32’ de latitude.

Nul doute que Mercator, en tout cas, ait ignoré la loi suivant laquelle il fallait graduer le méridien de la carte qu’il avait projetée. Et s’il eut l’idée de rectifier la loxodromie sur une carte à méridiens parallèles, il ne réalisa qu’incomplètement cette idée. Quelques auteurs ont même douté qu’il ait été le premier à construire approximativement des cartes réduites. Navarette prétend en effet qu’Alonzo de Santa Cruz en avait déjà construit, à la demande de Charles-Quint, seize ans an moins avant Mercator. Mais nous n’avons trouvé mention de ces cartes nulle part ailleurs.
La caractéristique la plus frappante de ces sortes de cartes est l’écartement croissant des parallèles quand on s’éloigne de l’équateur. Or l’idée de dilater le méridien de la sorte a pu venir à l’esprit de plusieurs indépendamment, cette dilatation étant une conséquence naturelle du fait qu’en traçant des méridiens parallèlement les uns aux autres on dilatait les parallèles et d’autant plus que la latitude était plus élevée. Mais le canevas de la carte loxodromique n’a été vraiment découvert que le jour où la règle suivant laquelle il fallait en chaque point du méridien, faire cette dilatation, à été enfin posée sous forme mathématique. Et c’est l’Anglais Edouard Wright, ami et collaborateur de Briggs, qui a nettement conçu cette règle et qui l’a le premier réalisée avec une approximation algébrique suffisante pour tous les besoins pratiques de la navigation. C’est d’ailleurs en méditant sur la carte de 1569 sur laquelle Mercator voulait effectivement représenter les loxodromies par des lignes droites, et à la suite d’un voyage aux Açores qui eut lieu en 1589 et qui lui donna l’occasion de se porter aux études de navigation que Wright, ainsi qu’il l’affirme, a été conduit à sa découverte. C’est cette carte qui lui a inspiré l’idée de corriger les erreurs de la Carte commune par l’augmentation des distances des parallèles quand on va de l’équateur vers le pôle, « de telle sorte, dit-il, qu’à chaque latitude une petite portion (small part) du méridien conserve avec la même partie du parallèle le rapport que ces éléments ont sur le globe ». Mais, ajoute-t-il, il n’a appris ni de Mercator, ni de personne la manière de le faire. La loi de la carte, la similitude des petites figures pour la conservation des angles, était enfin expressément et clairement énoncée. Voici des passages de son exposition d’après l’édition de 1657 (la troisième) de son ouvrage : Certain errors in navigation detected and corrected. Soit une sphère inscrite dans un cylindre. Gonflons la sphère comme en soufflant dans une vessie et toujours également dilatée en chacune de ses parties (c’est-à-dire partout autant en longitude qu’en latitude) jusqu’a l’appliquer sur le cylindre, chaque parallèle de la sphère devant s’accroitre d’autant plus qu’il est plus éloigné de l’équateur, de manière à devenir égal au diamètre du cylindre, donc égal aux méridiens de la sphère, lesquels seront également écartés jusqu’à être à chaque latitude à la même distance que sur l’équateur.

Dans un tel planisphère, où la surface de la sphère est également dilatée en chaque point aussi bien en latitude qu’en longitude, les méridiens, les parallèles et les rumbs (loxodromies) sont pareillement agrandis dans la même proportion, à toute latitude et les images des différents lieux sont dans les mêmes directions relatives que sur le globe. La carte conserve donc les angles : « the respective situation of all places each from other according to the points of the compasse is true ».

Il en résulte que les loxodromies sont des droites puisque les méridiens sont parallèles et qu’en chaque point le rapport d’un élément de méridien à un élément de parallèle est le même que sur la Terre. Et comme le parallèle devient un grand cercle l’élément de méridien à une latitude donnée φ devra être dilaté dans le rapport du grand cercle à la longueur de ce parallèle, donc multiplié par sec. φ. Des lors il était facile de calculer les longueurs successives des éléments du méridien de la carte. Wright prit d’abord le degré d’équateur comme élément initial m et il fit la longueur du degré de méridien compris entre 27 et 28° pour exemple égal à m séc. 28°. Puis il somma ces longueurs pour avoir les cotes des parallèles. Il envoya une première table ainsi construite à Blundeville avant 1594. Il se rendait compte d’ailleurs que plus l’élément initial choisi serait petit et plus il approcherait de l’exactitude, de ce que nous appelons l’intégrale. En 1599 donc il prit pour élément non plus le degré mais 10’. Enfin en 1610 dans sa seconde édition il prit la minute d’arc et il eut la patience de calculer les longueurs de toutes les minutes du méridien de la carte jusqu’à 89°59’ faisant toujours la minute comprise entre les latitudes φ et φ+1’ égale à sec. (φ + 1)’ ; ce qui, disait-il, donnait un nombre un peu trop fort. Il évaluait les sécantes jusqu’à la quatrième décimale. Il ne descendit pas à un élément plus petit que la minute, égal à 10" par exemple et il eut raison. En effet, l’erreur sur la latitude croissante de sa table n’est que de 0,8 sur 5.966 pour la latitude de 70° et elle n’est encore que de 2 unités un dixième à 80°, de 50 unités sur 107.646 à 85°, donc tout fait négligeable en pratique. Le calcul graphique correct du point estimé était cette fois une affaire achevée et consistante ; et il fut impossible de prétendre plus longtemps que la loxodromie à suivre pour aller d’un lieu A à un lieu B était différente de celle qui ramenait de B en A. Cela ne veut pas dire que la méthode ait été tout de suite comprise et acceptée, encore moins utilisée. Burrough, sur le vu de la carte de Mercator, déclara qu’elle était tout académique et faite pour des savants mais non pour des navigateurs ; Blundeville même n’en pensa pas beaucoup de bien et les chicanes ne manquèrent pas jusqu’à une époque tardive dans le XVIIIe siècle encore. Mais d’autres, et des meilleurs, reconnurent tout de suite son excellence.

 
Avant 1600 Iodocus Hondius, graveur d’Amsterdam, avait publié des cartes, sur le manuscrit de Wright, qu’il s’était procuré étant à Londres. En 1608 Stevin donna dans ses Hypomnemata Mathematica des tables de loxodromies, d’après Wright, pour permettre de construire ces courbes par points sur un globe. Ces tables permettaient aussi la construction par points des loxodromies sur la carte que Wright appelle « paradoxale » où les méridiens sont des droites convergentes et qui est propre, dit-il, aux navigations par hautes latitudes. Bouguer en parle encore pour mémoire. Stevin affectionnait les constructions sur les globes. Il avait proposé de tracer les arcs de grands cercles au moyen d’équerres orthodromiques et de même il indiquait la manière de construire des équerres loxodromiques par application sur un globe de lattes de cuivre le long de loxodromies tracées par points. C’est sans doute pour utiliser les lignes figurées sur les globes, en particulier les méridiens équidistants, qu’il modifia la construction approchée de Nunes en arrêtant l’arc AB par exemple (fig. 5) non au point B ou l’azimut orthodromique est devenu A + ΔA ; mais à sa rencontre en R’ avec le méridien du globe voisin du méridien de A et ainsi de suite. Il n’avait donc pas les points ABCD… mais des points R’S’T’… et ses équations différaient naturellement de celles de Nonius. Il semble qu’il ne comprit pas le procédé tout différent de ce dernier, car il l’accusa de s’être trompé. Le procédé de Stevin est d’ailleurs plus éloigné de la vérité que celui de Nonius. Snellius en 1624, Metius en 1631 marchèrent aussi sur les traces de Wright. De Stevin datent les mots loxodromie et orthodromie.

 
En France le P. Fournier avait bien compris les principes de la carte réduite. Il disait entre autres : « Les cartes de réduction croissant et allongeant les degrés des méridiens à même proportion que les degrés des parallèles, chaque terre en particulier retient sa figure. » Et il nous apprend que c’est un certain Le Vasseur de Dieppe, d’abord tisserand qui, sur les leçons de Cossin lequel « avoit une excellente main », « en a enseigné la pratique à nos François ». Il ajoute que les Hollandais ont apprécié ces cartes dieppoises et les ont imitées et il donne une table des cotes méridiennes, mais en prenant pour élément un arc de 10° d’équateur ajoutant, il est vrai, qu’en construisant un canevas avec ces longueurs « il y aura de l’erreur ».

 
Mais revenons à ce canevas au point où l’a laissé Wright. Avec lui nous n’avons pas encore une solution rigoureuse. On va voir par quels détours compliqués et assez surprenants cette solution a été enfin atteinte. Vers 1645 dans un Norwood’s Epitome, Henry Bond fit savoir qu’il avait découvert, on ne sait comment, que les cotes méridiennes de Wright étaient proportionnelles aux log. des tangentes des demi-latitudes augmentées de 45°. « On a d’abord découvert par hasard » ce rapport, dit Halley. Cependant Bond a dû être guidé, au moins en partie. De tout temps il y a eu des auteurs qui ont recherché des relations empiriques curieuses entre les nombres et il y aurait beaucoup à écrire pour épuiser ce sujet de la mystique des nombres. Bond était sans doute de ceux-là. Mais ici il y a plus. On cherchait à comprendre cette méthode de Wright assez délicate à entendre et à exposer et on cherchait un peu à tort et à travers. « Quelques-uns pensent qu’en substituant les tangentes au lieu des sécantes dont cette carte (réduite) est composée, on trouverait encore quelque avantage nouveau », lit-on dans le P. Fournier, contemporain de Bond. Et une figure de son Hydrographie pourrait faire croire, à qui ne lirait pas attentivement le texte qui l’accompagne, qu’il divisait le méridien par les tangentes des latitudes. Cela a plusieurs fois été proposé d’ailleurs et beaucoup plus près de nous. Peut-être est-ce une idée analogue qui a conduit Bond à chercher un rapport entre les cotes de Wright et une fonction des tangentes. D’autre part les logarithmes faisaient aussi depuis peu leur entrée triomphale dans le monde des mathématiciens. Bond avait donc des directions. En 1653 il ajouta à sa première remarque, qu’on obtenait la distance en degrés d’équateur entre deux parallèles donnés de la carte en prenant les log. des tang. de chaque demi-latitude augmentée de 45° et en divisant la différence des deux log. par log. tang. 45°30’. C’était une nouvelle concordance singulière, une simple rencontre cette fois, qui provient de ce que l’on a à très peu près, jusqu’à la 7e décimale : log. tg. 45°30’ = arc. 1° x log. e. Suivons maintenant Halley. Après avoir remarqué, inspiré par Bond, que les cotes en question étaient proportionnelles aux log. des tang. des demi-compléments des latitudes [car on a au signe près log. tg. (45° + φ/2) = log. tg. (45° - φ/2) ], il ajoutait que l’habile mathématicien Nicolas Mercator avait trouvé la démonstration de ce théorème si difficile, qu’il avait proposé de parier une grosse somme d’argent contre n’importe qui, qu’il était impossible également soit de démontrer qu’il était vrai, soit de prouver qu’il était faux. Mais en l668 James Gregory l’établit pour la première fois ; seulement il le fit avec un enchainement de raisonnements si compliqués qu’on y perdait le fil de la démonstration et qu’on était excédé, « wearied out », avant d’arriver au bout, dit Halley. Ce dernier alors entreprit une nouvelle démonstration qu’il publia en 1695 dans les Philosophical Transactions. Il remarqua tout simplement que la projection stéréographique d’une loxodromie sur l’équateur était une spirale logarithmique et de cette propriété il déduisit enfin l’équation de la courbe qui exerçait les chercheurs depuis plus de 150 ans.

 
Enfin, une vingtaine d’années plus tard, en 1714, Roger Cotes apportait une dernière amélioration à la méthode de Halley en simplifiant sa démonstration. Cotes, astronome et physicien, ami de Newton, est l’auteur des formules différentielles des triangles et le premier à les avoir utilisées pour la recherche des circonstances favorables. Ainsi, grâce à Wright, les navigateurs pouvaient résoudre aisément sur la carte tous les problèmes de l’estime. Wright savait en particulier comment on pouvait avoir une distance loxodromique exacte en construisant sur l’échelle des longitudes le triangle rectangle déterminé par la différence des latitudes des points de départ et d’arrivée et l’angle de route, triangle dont l’hypoténuse était la distance cherchée (φ2 – φ1 = m cos V). Il avait aussi calculé une table des rumbs (loxodromies) permettant de les tracer par points sur un globe ou sur une carte quelconque. Cette table donnait pour chaque rumb la latitude des points d’intersection du rumb et des méridiens successifs. Il fit en outre remarquer que la table de ses divisions méridiennes permettait de résoudre très exactement par le calcul les problèmes de l’estime ; mais il ne jugea pas utile de rechercher cette exactitude étant donnée l’imperfection des données, en particulier les erreurs sur les angles de route. Mais bientôt, en 1614, Raphe Handson donna une solution très claire de tous les calculs que comporte le point estimé en utilisant la table de Wright, C’est de lui aussi de plus que datent nos méthodes approximatives de calcul, qui ne nécessitent pas le recours aux latitudes croissantes. Handson proposa en effet de déterminer le changement de la longitude soit au moyen de la moyenne arithmétique entre les cosinus des latitudes, soit par la moyenne entre les sécantes des latitudes. Cette dernière méthode était d’ailleurs plus incorrecte que la première ainsi qu’il s’en était assuré. Mais c’est dans les œuvres de Gunter, publiées en 1623, qu’on trouve pour la première fois la méthode par la latitude moyenne dont on use depuis comme on sait parce que c’est la plus commode.

Ces différentes méthodes furent comparées entre elles et on trouva que la moyenne arithmétique entre les cosinus était préférable à la latitude moyenne par hautes latitudes. Un autre auteur, Bassat, avait proposé la moyenne arithmétique entre les log. des cosinus.   Nos tables usuelles firent ainsi leur apparition et remplacèrent les anciennes. Parmi ces dernières nous indiquerons la table suivante de Medina, conçue assez heureusement pour les besoins de la marine à voile. Soit un bâtiment B voulant atteindre le point A (fig. 7). Il suit une route BC faisant en B un angle V avec BA. Quand il relève A à l’angle V’ il est en un certain point M. La table donne, dans trois colonnes, les valeurs correspondantes de BM, AM et (l’angle) MAB. II y avait autant de tables que d’aires de vent V. Quant à la « table de point » qui se trouve aujourd’hui dans tous les recueils de tables nautiques, elle apparait chez Norwood. D’autre part des tables loxodromiques sont publiées alors dans presque tous les traités. Celles d’Adrien Metius se retrouvent encore dans l’édition de 1679 du P. Fournier. Pour chaque aire de vent elles donnent les éléments suivants. La loxodromie ayant son point de départ sur l’équateur, trois colonnes donnant la latitude et la longitude atteintes après avoir parcouru une certaine distance loxodromique exprimée en lieues d’Allemagne, ce qui s’explique par la nationalité de Metius, de 15 au degré. On rencontre encore d’autres tables, par exemple celle chez Wright donnant la distance parcourue à chaque aire de vent pour une variation de la latitude de 1°. Or la latitude était déterminée directement. Signalons enfin que la table de point pouvait être remplacée par le quartier de réduction dont le treillis quadrangulaire figure déjà sur des astrolabes du moyen âge et auquel en France, en 1671 Blondel de Saint-Aubin consacrait un livre spécial : L’Art de naviguer par le Quartier de réduction.

Mais les pilotes ne se précipitaient pas avec enthousiasme, semble-t-il, sur tous ces perfectionnements : « Nos mariniers français, est-il écrit dans l’Hydrographie n’ont encore aucun usage des tables loxodromiques par lesquelles on vient à bout très facilement des problèmes de l’estime. » Plus tard il est vrai ils dépassent vraiment la mesure dans un autre sens. Les pilotes en effet trouvaient des différences entre la latitude d’arrivée, calculée par l’estime, et la latitude observée à midi. Il eut fallu se contenter d’adopter comme point la latitude observée et la longitude estimée. An lieu de cela ils voulaient déduire une erreur sur la longitude de l’erreur sur la latitude. Rien de plus fatigant ni de plus fastidieux que de lire les innombrables règles et exemples qu’on trouve à ce sujet dans les traités de navigation du XVIIIe siècle. Presque tous s’occupent de la question. Bouguer et Bezout ne s’en dispensent pas. Gaigneur parait s’y complaire, il est le plus abondant. On admettait, suivant les cas, distingués par la direction de la route, que l’erreur sur la latitude provenait du loch ou du compas exclusivement, ou des deux à la fois, dans une certaine proportion ; et on calculait alors aisément la prétendue erreur sur la longitude. Or, l’appréciation qui servait de base au calcul était tout à fait arbitraire et fantaisiste. Les erreurs provenaient sans doute en partie de la grossièreté des instruments ; seulement elles étaient par essence inestimables et on ne devait pas par suite toucher aux résultats en les évaluant à vue. Elles provenaient surtout de la dérive et des courants, qui étaient absolument inconnus et qu’on ne savait apprécier. Aussi est-ce une véritable satisfaction que de rencontrer des auteurs jugeant sainement ces sortes de corrections. Déjà le P. Fournier qui ne consacre que quelques lignes à la question, malgré sa prolixité habituelle, conclut en disant que lorsqu’un trop grand écart entre les deux latitudes observée et estimée devient dangereux pour la navigation,le mieux est de mettre sa confiance dans le « saint patron du navire ». Plus près de nous Chabert, par exemple, écrit en 1753, que la correction qu’on a coutume d’apporter à la longitude d’après l’erreur sur la latitude, est quelquefois une nouvelle source d’erreurs ; car on ne sait d’où provient l’erreur sur la latitude ; il est du sentiment de ne jamais corriger les lieues est et ouest et de prendre la latitude observée et la longitude estimée. La Caille aussi ne parle de ces questions que pour s’élever en peu de mots contre ces opérations « abritraires des pilotes » ; et il pense qu’ « on doit corriger seulement la longitude quand on a des données précises sur les courants ». Mais Rossel, en 1814, n’ose pas encore supprimer les passages de Bezout qui sont relatifs à ces singuliers procédés. Seulement il se contente de mettre en note des remarques analogues aux précédentes.

 
A la suite de Bezout d’ailleurs, il avait laborieusement donné des formules destinées à tenir compte de l’ellipticité du méridien terrestre, bien mal connue à l’époque, dans les calculs de l’estime. On souhaiterait un peu plus de jugement. Bezout n’était du reste pas ici un initiateur. Il avait eu pour prédécesseurs Don J. Juan qui faisait partie de la mission de 1735 à l’Equateur. Mendoza, du Bourguet s’en occupèrent aussi. Enfin Delambre énonça l’élégante remarque d’après laquelle il suffit, pour tenir compte pratiquement de l’ellipticité, de remplacer la latitude géographique par la latitude géocentrique.

 
Concluons toutefois, à la décharge de ces médiocres théoriciens, que s’ils se débattaient ainsi devant des difficultés sans issues, cela mesurait l’importance qu’ils attachaient, à juste titre, au problème dont ils désiraient une solution.

 
On peut ici dire un mot de l’orthodromie. Elle avait peu d’intérêt pour la marine à voiles où les vents surtout et les courants déterminaient les routes et n’offrait d’ailleurs aucune difficulté théorique. Aussi ne s’en occupe-t-on à peu près pas avant le développement de la marine à vapeur. Wright cependant indiquait déjà un moyen géométrique direct d’avoir la distance orthodromique. En 1838 Caillet commence à en parler dans ses leçons à l’École Navale ; il recommande le tracé du grand cercle par points sur la carte marine et il propose de construire en transparent les images des grands cercles passant par deux mêmes points de l’équateur ; images qu’il suffira de superposer sur une carte de mêmes dimensions, par glissement des équateurs l’un sur l’autre, de manière à ce que les deux points donnés de la carte se trouvent sur une même orthodromie, pour résoudre tous les problèmes particuliers ; idée qui a été reprise et réalisée par le Service Hydrographique il y a quelques années.

 
Note. – Sur un globe de 30 c/m environ de diamètre, avec méridiens équidistants de 15°, j’ai tracé, à main levée, armé simplement d’un rapporteur transparent ordinaire, d’ailleurs trop grand, et d’un crayon en allant de méridien en méridien, les deux loxodromies de 60° et de 40°, la première sur un parcours en longitude de 180°, la deuxième de 90°. Je suis ainsi arrivé aux latitudes de 71° et de 72°50’ en erreur sur les latitudes exactes de 30’ et de moins de 25’. Ces erreurs sont plus faibles que celles des loxodromies du globe de 1541. J’ai fait ces tracés sans application excessive et rapidement de sorte qu’il m’eût été facile de mieux faire. D’autre part l’erreur de 158 unités de la table de la page 46 correspond, sur la latitude, à une erreur de 53’, et cette erreur serait plus grande d’après les nombres de Blundeville. Ainsi Mercator n’était pas nécessairement un dessinateur très habile et il a pu construire sa carte de 1569 sur un tracé à main levée assez grossier. Mais il a pu aussi bien, comme on l’a vu, employer le procédé de Nunes, qui avait l’avantage de lui donner une garantie géométrique et c’est peut-être ce qui l’a décidé.

II. - Les résultats

Avec la manière d’obtenir les éléments de l’estime, les erreurs sur la dérive, l’ignorance des courants, les faibles vitesses et les durées des traversées, les vents variables, l’abus des calculs graphiques, on trouvera naturelles les énormes erreurs que l’on rencontre dans la position estimée du navire. En voici des exemples pris surtout dans le XVIIIe siècle. Elles étaient pires auparavant.

• Christophe Colomb, dans un rapport sur son quatrième voyage, fait aux Monarques Catholiques. accuse déjà les pilotes de se tromper de plus de 400 lieues, soit de plus de 20°.
• Dans sa campagne de 1722 sur les bancs de Terre-Neuve, Radouay trouve qu’à l’aller, à l’atterrage sur les bancs, les points des pilotes se sont tous faits, par suite de l’imperfection de leur loch, en erreur au moins de 80 lieux de 5.555 mètres sur l’avant du navire, et Bouguer dit que quand on a des vents contraires les erreurs atteignent souvent 7° à 8°.
• Le 14 novembre 1764, Chappe lit à l’Académie un rapport sur les épreuves de la montre n° 3 de Ferdinand Berthoud. C’était le premier du genre. Il y rappelle les observations de La Caille dans son voyage au cap de Bonne-Espérance. Ce dernier était parti sur le Glorieux, commandé par d’Après de Mannevillette. Trois semaines plus tard, ils cherchaient l’île San Yago du Cap Vert, en faisant route à l’ouest, car ils s’en croyaient à l’est. Mais en réalité ils en étaient à l’ouest, avec une erreur en longitude de plus de 4°, ce qui les obligea à relâcher à Rio de Janeiro, car ils ne pouvaient revenir en arrière et ils avaient besoin de caréner un petit bâtiment de leur suite qui avait une voie d’eau considérable. D’Après signale aussi le cas fréquent des navires qui, se croyant à Ténériffe, atterrissaient au cap Noun, à 5 ou 6° de distance de cette île, d’où on concluait que les courants portaient à l’est. Le 8 mars 1753, La Caille quitta le Cap pour les Mascareignes. A la fin de la traversée, l’estime les mettait à 40 lieues à l’est de Rodrigue, alors qu’ils en étaient à 180.
• Harmanzen, en 1602, se croit à Maurice et est à Rodrigue, à 5°5 plus à l’est.
• Chappe s’étend sur les inconvénients pour les navires d’avoir de mauvaises longitudes. Il cite une erreur de 179 lieues faite en 1763 par un « de nos meilleurs pilotes » dans une traversée de France à la Guyane française, et une autre de 150 lieues dans un second voyage entre les mêmes points. La même année, une erreur de 200 lieues est commise par un bâtiment, vers les Bermudes ; et un autre se trouve vers le fleuve des Amazones se croyant en haute mer.
• Cassini le fils, sur l’Enjouée, effectuant en 1768 un voyage de circumnavigation dans l’Atlantique nord, pour étudier les montres de Le Roy, annonce que les meilleurs navigateurs disent commettre des erreurs de 50 à 60 lieues en deux mois.
• Dans le voyage de la Flore, en 1772, on remarque des erreurs de 56’ sur une traversée de cinq jours, du 25 au 30 janvier 1772, de Gorée à la Praya ; et une autre de 2°17’ du Cap Français à Saint-Pierre et Miquelon, en vingt jours.
• L’examen du journal de Suffren de 1781 à 1784, démontre qu’ils commettaient des erreurs de même ordre. On observait de temps en temps des distances lunaires dans son escadre, ce qui donnait une idée des erreurs de l’estime. A l’aller, ils se trouvent en avance de 6° sur le point estimé quelques jours avant d’atterrir au Cap, au moment de couper le méridien de Paris, une vingtaine de jours seulement après avoir quitté La Trinité. Au retour, de la côte de Coromandel à l’île Rodrigue, en novembre 1783, ils ont des erreurs de 5°, l’estime les mettant de cette quantité en arrière de leur vraie position. Par contre, de l’Ile de France au Cap, en décembre de la même année, l’estime les met dans l’intérieur du continent africain, à environ 50 kilomètres de la côte, alors que les bâtiments que Suffren envoie en avant de l’escadre pour chasser la terre n’aperçoivent rien. Nous avons trouvé dans un manuscrit d’un officier du génie qui partit de Brest le 11 février 1782 avec des bâtiments de renfort pour l’armée de Suffren, qu’avant l’atterrissage au Cap, les vaisseaux de guerre qui ont fait des observations de longitude se croient à 100 lieues (5°) du Cap alors que l’estime les met tout près de terre.
• Pendant la campagne de d’Estaing dans l’Amérique du Nord, en 1778-1759, au moment de la guerre de l’indépendance américaine, Chabert observe des longitudes. Vers le milieu de la traversée de Toulon à la Delaware, il reconnait que l’estime des pilotes était fautive de près de 6° dont leur route était trop peu avancée. D’après les observations, l’armée avait dépassé le méridien des Bermudes et elle put franchir en sécurité le parallèle de ces îles, en passant à l’ouest, alors que l’estime indiquait dans ce parti une manœuvre dangereuse. La traversée, qui fut très longue, en fut heureusement raccourcie.
• Fleurieu relève soigneusement les erreurs de l’estime dans le voyage autour du monde du capitaine marseillais Marchand, de 1790 à 1792. Dans la traversée du Cap Vert à la Terre des Etats, leur longitude estimée est en erreur, en dix jours, du 26 février au 8 mars, de 3°46’. Dans la traversée totale, qui dura 73 jours, ils ont à l’arrivée une erreur résultante de 7°6’, provenant d’erreurs en retard montant au total à 6°29’ et d’erreurs en avance formant une somme de 13°35’. De la Terre des Etats à l’île Mendoça, par φ = -10° et g= 141° W., en 73 jours encore, la somme des erreurs est de 8°41’ vers l’est, de 4°13’ vers l’ouest ; donc à l’atterrage elle reste de 4°28’. Disons encore qu’à la fin du voyage de l’île de la Réunion à Sainte-Hélène, en 43 jours de mer, l’erreur à l’atterrissage estimé aurait été de 8°, soit de 850 kilomètres environ : dimension de la France sur le parallèle de Brest.
  • Voilà ce qu’on trouvait avec le loch et le compas. Le bâtiment zigzaguait de part et d’autre de la route estimée qu’il croyait suivre ; s’en écartant parfois à de très grandes distances ; et le danger qu’il courait de ce fait est évident. Aussi, lit-on dans Marchand, « qu’il faut rendre hommage aux sciences et aux arts qui, en soustrayant le navire à l’empire de l’arbitraire, ont fourni des moyens assurés pour se mettre à l’abri des redoutables effets d’une incertitude à laquelle le marin le plus habile opposait vainement sa longue expérience ».

Lorsque de simples retards résultaient de ces à peu près, leurs inconvénients étaient peu graves et ils ne laissaient pas de trace. Mais les conséquences des erreurs de l’estime s’étendaient plus loin et devenaient une source permanente de dangers. L’estime ne servait pas seulement à faire le point ; c’est aussi par les moyens imparfaits qu’elle mettait à la disposition des navigateurs qu’étaient dressées les cartes dont on se servait à la mer. Jusqu’à la fin du XVIIIe siècle, en effet, la plus grande partie de ces cartes était basée sur des positions estimées ; et il ne pouvait en être autrement, parce que la détermination très exacte des coordonnées géographiques nombreuses, nécessaires à une cartographie complète et précise, au moyen d’observations astronomiques et géodésiques faites à terre, est une entreprise immense. C’est pour cette raison, entre autres, que la table des positions géographiques de la Connaissance des Temps ne contient, en 1745, encore, que celles de 140 lieux ; qu’en 1749 il n’y en a que 205 et en 1778, 228 seulement.

• Dans la mappemonde d’Ortelius, de 1587, 10 différences de longitudes sont en erreur absolue moyenne de 7°5 ; l’erreur est de 17° entre Gibraltar et Shanghai, de 12° entre Gibraltar et le cap Comorin, de 7° entre Gibraltar encore et le cap des Aiguilles. Ces trois dernières différences sont toutes trop grandes sur la carte. De même la Méditerranée est allongée de 9°. Dans le Haven finding art de Simon Stevin, qui vaut pour 1610 environ, dix autres différences de longitudes se montrent en moyenne en erreur de 6°5 ; les plus grandes erreurs allant à 12° entre Londres et Goa d’une part, Londres et Canton d’autre part.
  • Les longitudes y sont comptées de Corvo des Açores qui est donnée à 3° trop distante de Londres.
• Voici maintenant ce que Chabert, dans un Mémoire de 1759, dit des cartes de la Méditerranée. Quand ou commença, en 1679, sur les ordres de Colbert, à travailler aux cartes de cette mer, ou observa simplement des latitudes à l’astrolabe et à l’arbalestrille ; on releva au compas les directions allant d’un cap au cap voisin, et on mesura au loch leurs distances respectives. Les officiers prétendaient que les observations astronomiques à terre étaient inutiles, puisque le marin voyait les côtes du large. C’était en particulier l’opinion de Tourville, en 1685. Aussi relève-t-on des erreurs de 30’ en latitude sur les cartes publiées à Marseille en 1689, et jusqu’à cette époque, la Méditerranée était allongée en longitude du quart au septième de sa longueur.
• Les parages du Grand-Banc de Terre-Neuve, où, d’après le voyage de Cassini déjà cité, on pratiquait depuis longtemps, comme de nos jours, la pêche à la morue, étaient très fréquentés. Pourtant Radouay, en 1722, estime que la position du Grand-Banc est en erreur de 80 lieues en longitude ; et Chabert, en 1750-1751, écrit que jusqu’alors les cartes de la région de Terre-Neuve étaient toutes « fondées sur l’estime ». Il fait remarquer qu’entre les cartes anglaises et hollandaises il y a une différence de 9° ou 120 lieues dans la position de la côte orientale de Terre-Neuve, soit une erreur de un sixième sur la distance de l’île aux côtes d’Europe. Il a déjà fait en 1746 deux campagnes en Acadie et il a été témoin alors des dangers courus dans ces parages par plusieurs vaisseaux, notamment par quelques-uns de ceux qui faisaient partie de la malheureuse escadre de l’incapable duc d’Anville. Et c’est pourquoi il a formé le projet de s’instruire en astronomie, avec la perspective des grands effets que devait produire l’application des officiers de marine à cette science. C’est ainsi qu’il devint géographe.
• Chappe se rendant en Californie, en 1761, trouve que la longitude de la Vera Cruz est fausse de 3°. Dans la relation du voyage de Fleurieu, sur l’Isis, en 1768 et 1769, le nombre des erreurs relevées sur les cartes de l’Atlantique nord est innombrable. Les cartes de Bellin, du Dépôt des cartes et plans de la Marine, sont très inexactes, y est-il dit. Citons l’île de Mai, dans les îles du Cap Vert, qui est un degré trop à l’est ; la Martinique, qui a quatre positions sur quatre cartes différentes ; les Açores. dont la plus occidentale est en erreur de 3°75 vers l’est sur une carte, de 0°66 vers l’ouest sur une autre, de sorte que la différence des deux est presque de 4°5. Du reste, aucune n’est exacte. Mêmes plaintes chez Verdun, deux ou trois ans plus tard : « Nous eûmes de la peine à trouver l’Islande (ils venaient du Grand-Banc) ; sur l’autorité des cartes, nous la cherchions plus à l’ouest. » Les erreurs sur la position de cette grande île étaient énormes. Les cartes de Bellin, les plus exactes, mettaient Patrix fjord par 30° de longitude, au lieu de 26°4 et par 66°15’ de latitude, au lieu de 65°36’. Il se passa sept jours entre les premiers sondages de Verdun et le moment où il vit enfin la terre. Les brumes fréquentes leur imposaient, il est vrai, une grande prudence. Et Fleurieu remarque avec amertume que l’Atlantique nord est pourtant la partie du globe la mieux connue.
• Passons à l’Atlantique sud et à la route des Indes Orientales, avant les immenses travaux de d’Après de Manevillette. Sur un globe terrestre de 1648, conservé au Musée Maritime de Brest, la distance en longitude entre le Cap Vert et le cap de Bonne-Espérance est en erreur de 6° ; mais Améric Vespuce mettait le Cap sur le méridien d’Alexandrie, commettant une erreur de 11°5. Et en 1685, deux cents ans après la découverte du cap de Bonne-Espérance, qui était devenu un véritable boulevard maritime, sa longitude n’était encore fixée que par l’estime. Cette année-là, les savants Jésuites d’une ambassade au Siam profitèrent de leur séjour dans la baie pour faire quelques observations astronomiques. Ils s’installèrent dans le beau jardin de la Compagnie des Indes hollandaises et fixèrent pour la première fois, par des observations célestes, la longitude de ce point si important. Mais ils n’eurent qu’une émersion du premier satellite de Jupiter, le 4 juin 1685 et ils en conclurent pour la longitude du Cap, par rapport à Paris, la valeur de 17°44’5, en erreur de plus de 1°5. C’était à peu près la longitude de la carte de La Hire ; une autre carte, de Du Val, donnait 22°30’, en erreur de 6°. Les navigateurs s’aperçurent, parait-il, que la nouvelle longitude des Jésuites ne s’accordait pas avec les routes faites du Cap Sainte-Hélène dont la longitude avait été bien déterminée par les astronomes anglais. La Caille, en 1751, par des éclipses de Lune et des satellites de Jupiter, et par des occultations, trouve enfin la vraie valeur, qu’il fixe à 16°10’. Il montre aussi que les jésuites se sont trompés de 20’ sur la latitude du même point.
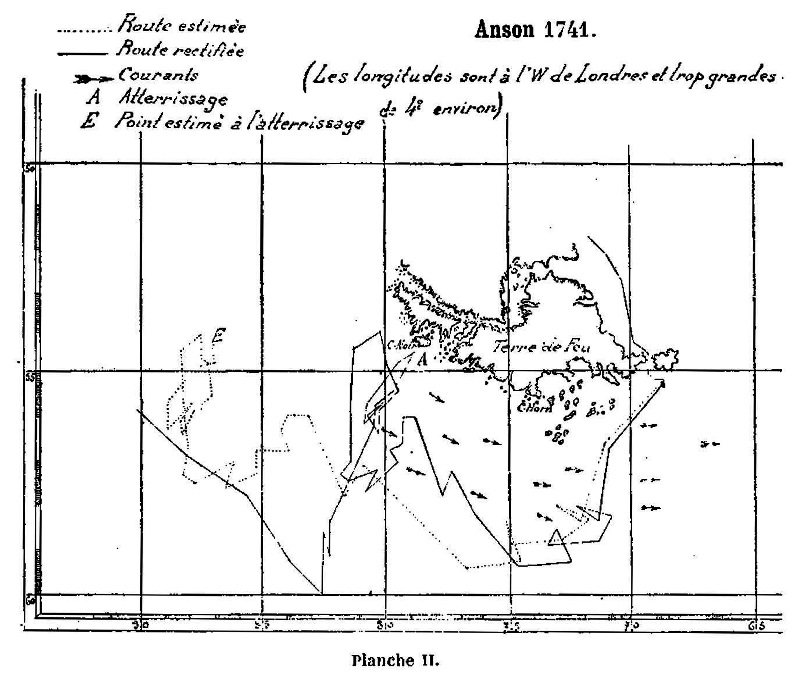
• Les régions du cap Horn, où se rencontraient beaucoup de navires, étaient encore plus mal connues. Vers 1700, les armateurs malouins commerçaient activement avec les ports de la côte Pacifique de l’Amérique du Sud. De 1712 à 1714, un ingénieur du roi, Frézier, poussé par un grand désir de voyager, s’embarqua sur un bâtiment de Saint-Malo pour visiter les villes du Chili et du Pérou. II donne 61°35’ de longitude au détroit de Maire, au lieu de 67°30’, et fait remarquer que les cartes mettent d’ordinaire 100 lieues de ce détroit au cap Horn. Il raccourcit cette distance à 40 ou 50, ce qui était encore trop, puisqu’il n’y en a que 30. Les cartes donnaient au cap Horn une latitude de 57°5 ou 58° au lieu de 55°43’, valeur exacte. Quant à Lemaire et Shouten, les premiers à l’avoir doublé en 1615, ils lui donnèrent une latitude de 57°48’. C’est dans ces parages encore qu’Anson, en 1741, eut une erreur de 8 à 10°, sur son estime, du 7 mars au 14 avril, entre le détroit de Lemaire et le cap Noir, au S. W. du détroit de Magellan (Planche II).

 

 

Les petites îles isolées étaient si mal placées que souvent elles étaient dédoublées ou multipliées davantage.

• Une île, appelée Nouvelle Sainte-Hélène, fut longtemps figurée, à l’est exactement de la vraie Sainte-Hélène, à 9° sur certaines cartes. On croyait si bien à son existence, qu’après l’occupation de Sainte-Hélène par les Anglais, la Compagnie Hollandaise la fit rechercher par une expédition militaire destinée à en prendre possession. Toutes les Compagnies des Indes avaient alors besoin de « points de rafraîchissement ».
• L’île de la Trinité, par 20°5 de latitude sud, était à la fois sur les routes d’aller et de retour d’Europe aux caps Horn et de Bonne-Espérance. Aussi fut-elle déquadruplée. On prétendait qu’il existait à l’ouest, à une centaine de lieues, une autre île, nommée l’Ascension de l’Ouest. D’après la tradition, elle aurait été découverte en 1501 par Jean de Nove. Cependant Castanheda plaçait par 8°, au lieu de 20, l’île découverte par ce navigateur. On en donnait des descriptions détaillées. Il y avait dans le nord une anse où tombait une rivière, et une caverne où entrait la mer. (La Trinité a en effet une arche remarquable au bout d’une plage, mais à l’est.) On la trouve sur la mappemonde dessinée en 1587 par le Flamand Ortélius, d’Anvers, accompagnée vers l’est, et sur le même parallèle, de trois îles espacées de quelques degrés les unes des autres. Le routier portugais la plaçait, dit d’Après, sur la latitude même de la Trinité. Les Portugais figuraient également des îles à l’est de ce dernier îlot : les Martin-Vaz, à 120 lieues (6°) et Santa Maria d’Agosta dans leur voisinage. Et de même faisait le P. Du Val, géographe du roi, dans sa mappemonde de 1683, où d’autre part l’Afrique est extraordinairement élargie. Frézier, à son retour, touche à cette île de l’Acençaon, dont on orthographie le nom à la portugaise, dit-il, pour la distinguer de l’Ascension d’Afrique. Il remarque qu’on peut la reconnaitre à trois flots qui en sont très près, à l’est, « ce qui a donné occasion de croire que cette île et celle de la Trinité n’étaient que la même ». Il n’ignore pas que des vaisseaux ne l’ont pas trouvée ; mais il sait aussi que d’autres l’ont reconnue en revenant des Indes Orientales, et qu’ils y ont fait de l’eau dans un étang. « C’est donc mal à propos », d’après Frézier, qu’Halley, qui l’avait vainement recherchée vers 1700, « l’a supprimée sur ses cartes ». Olivier Van Koort était aussi allé à sa découverte en 1599. La Compagnie française des Indes la fit également et toujours en vain rechercher par l’Oiseau et l’Hirondelle en 1731 ; et elle recommença en 1739. En 1752, une fois de plus, elle ordonna à d’Après, qui rentrait en France, d’aller à sa découverte. Celui-ci navigua sur le parallèle de l’archipel sans trouver ni les unes ni les autres ; et il revint convaincu que seuls existaient la Trinité et, à l’est de celle-ci, quelques rochers très rapprochés d’elle, à 15 ou 20 milles. Cependant, à son passage à Rio de Janeiro, des capitaines lui avaient affirmé avoir relâché aux îles Martin-Vaz et y avoir fait du bois et de l’eau « dont elles sont abondamment pourvues », ajoutaient-ils, Une dizaine d’années après, d’ailleurs, il croit de nouveau à l’existence de l’Ascension de l’Ouest parce qu’en 1760 Duponcel-la-Haye, de la même Compagnie que lui, allant de l’Ile de France à Rio de Janeiro, affirmait avoir reconnu la Trinité, puis l’Ascension, à 100 lieues (5°) à l’ouest, un peu plus au sud toutefois, et avoir ensuite atterri au cap Frio d’Amérique. Et Suffren, en 1781, se servit des estimations de Duponcel-la-Haye pour fixer la longitude de la Trinité. Il l’avait exactement déterminée par l’observation de distances lunaires ; mais il choisit comme longitude véritable la moyenne entre son résultat et l’estime de Duponcel et commit, ce faisant, une erreur de 1°25.
  • L’histoire de l’Acençaon n’était pas finie. En 1784, le gouverneur général du Brésil essaya de la retrouver encore et Lapérouse, en 1785 ; Krusenstern, en 1801 ; Freycinet en 1817 la recherchèrent de nouveau. Cette même année, Devaux, comptant sur son existence, faillit périr. II commandait la Jeune-Sophie, destinée à Bourbon. Or, arrivé vers l’île de la Trinité, ce bâtiment, qui portait du vitriol, eut un incendie à bord, et Devaux, dépassant cette île, et « regardant l’Ascension comme un dernier refuge », se résolut tout d’abord à tenter d’atterrir à Rio pour sauver son bâtiment. Mais le feu prit de telles proportions qu’il revint en arrière et s’échoua sur la Trinité. Elle était d’ailleurs supprimée alors sur les cartes françaises, anglaises et portugaises. Cependant le général Milet-Mureau, du corps du génie, rédacteur du voyage de Lapérouse n’était pas convaincu de son inexistence, car l’enseigne Lépine lui avait assuré avoir relâché à la Trinité et à l’Acençaon.
  • Enfin, le 20 avril 1826, Bougainville le fils s’en trouve à 40 lieues à l’est ct regrette de ne pouvoir, faute de temps, faire de nouvelles recherches « bien que l’opinion généralement reçue aujourd’hui, dit-il, est que cette île n’existe pas ».
• Naturellement le cas de l’Acençaon n’est pas isolé. Dans le traité de Bouguer de 1753, figure une île Saint-Mathieu, sous le cap des Palmes, au sud et très près de l’équateur. Elle se trouve à 10° environ à l’ouest de San Thome et n’a naturellement jamais existé. Elle passait pour avoir été découverte le 15 octobre 1525 par Loaysa, le même qui fut le premier à apercevoir le cap Horn, qui la décrit avec une précision qui n’est pas sans déconcerter : « couverte de végétation ayant un bon mouillage » et située par 2°5 de latitude sud. Il dit y avoir séjourné pendant 18 jours et qu’on y trouvait deux arbres dont les incisions de l’écorce indiquaient qu’en 1435 déjà les Portugais avaient passé par là. On y ajoutait qu’un bâtiment du quatrième voyage de Vespuce y avait fait naufrage. Faut-il y voir un double de l’une des îles du fond du golfe de Guinée !
• Le Pacifique avait aussi ses îles doubles ou multiples. Sur une carte du récit des voyages de Marion et Surville dû à Rochon, et qui est de l’an VIII, on trouve deux archipels à l’ouest exactement des Galapagos, à 6° et à 12° de ces îles. Le plus occidental s’appelle Gallego. Ce nom est encore celui d’une île unique portée à peu près à l’emplacement de l’archipel le plus ouest de Rochon, un peu plus au N. W, toutefois, sur une carte de Duperrey parue en 1829. Citons enfin l’archipel de Los Majos et îles environnantes, qui jusqu’à Lapérouse doubla les Sandwich à 16 ou 17° à l’est. On y compte neuf îles pour le moins sur la carte du Pacifique du tour du monde d’Anson, qui eut lieu de 1740 à 1744. Cette carte est d’ailleurs des plus fantaisistes, en particulier dans la représentation du Japon.

De semblables erreurs s’expliquent très simplement. Les îles fictives sont toujours sur la même latitude que les îles réelles, et les distances qui les en séparent sont toujours du même ordre que les erreurs de l’estime. II faut donc attribuer leurs prétendues découvertes aux erreurs sur la longitude estimée. A cause de ces dernières, le navigateur qui voyait une terre, se croyait à l’est ou à l’ouest de quelques degrés de sa vraie position et il portait une nouvelle île sur la carte. Ainsi la partie pélagique des océans était en quelque sorte figurée plusieurs fois, les diverses représentations pouvant se ramener les unes aux autres par des glissements le long des parallèles.

 
Chappe dit du bâtiment qui avait commis une erreur de 100 lieues dans le voisinage des Bermudes que c’est miracle qu’il ne se soit pas échoué sur des écueils qui se trouvent dans l’est de l’archipel à cette distance. Ces roches sont en effet portées encore sur les cartes jointes au voyage de Verdun, éditées en 1778. Or, à 100 lieues à l’est des Bermudes, il n’y a que des fonds de 4.700 mètres.

 
Les cartes étaient encore compliquées par les vigies dont elles étaient abondamment semées. C’étaient des écueils qu’on croyait avoir aperçu en haute mer et qu’on signalait sans avoir pris la peine d’en vérifier l’existence ; faute le plus souvent de moyens de le faire avec exactitude. Ces écueils n’existaient pas, n’étaient pas un danger par eux-mêmes ; mais, comme ou cherchait à les éviter, ils compliquaient la navigation. Nous avons recherché quelques-unes des nombreuses causes auxquelles on peut les attribuer. II y a d’abord les erreurs de l’estime qui ont fait mal placer une terre réellement aperçue. Puis, d’Après parle de coups de tangage violents qui font croire quelquefois aux navigateurs qu’ils ont touché. Voici une troisième cause.

• Dans le journal de bord de Suffren, on lit que le 17 octobre 1781, l’armée faisant route pour la côte de Coromandel, « on a cru voir des brisants au N.N.O. ». Mais on sonda un quart d’heure sans rien découvrir ; « notre erreur, est-il dit alors, est surement provenue des rayons du soleil qui donnaient dans cette partie ». Ces sortes d’illusions peuvent donc avoir fait croire à une vigie.
• Relatons maintenant une observation que nous devons à Chabert. A son retour du voyage de 1751, étant à 70 lieues de Corve et Flore, à l’ouest des Açores, ils aperçurent sur l’eau quelque chose de noir autour duquel volaient des goélands, qu’ils prirent pour des rochers, même à la lunette. Mais il n’y avait pas de brisants. On alla à la reconnaissance en canot et on découvrit que ce n’était qu’une baleine pourrie d’une grosseur monstrueuse. « Si on ne s’était pas assuré du contraire, fait-il remarquer, beaucoup de personnes seraient restées persuadées qu’on avait rencontré une vigie. » D’ailleurs la plupart des marins, Bougainville par exemple, pensaient que la vue de bandes d’oiseaux indiquait la proximité d’une terre ou d’une vigie.
• Humboldt remarque que l’usage irréfléchi d’itinéraires fictifs ou mal rédigés fait naître des doubles emplois sur les cartes et il ajoute – nous sommes en 1837 – que : « la multiplicité des vigies dont l’Atlantique était couverte, il y avait soixante ans, rappelait cette source d’erreurs. Cela ne l’empêche pas de placer entre l’île de Pâques et Juan Fernandez, les Sporades de Pilgrim ct de Warehams rocks, qui sont purement imaginaires et de n’être pas loin de croire à la réalité de brisants que des navigateurs espagnols prétendaient avoir découvert en 1802 par 28° de latitude nord et 43°22’ à l’ouest de Paris. Mais nous savons que pareilles méprises se reproduisent de nos jours.
• Il faut conter ici l’histoire de saint Borodon on saint Brandon. Elle est placée sur le globe de Behaim de 1492, avec l’indication « c’est l’île ou saint Brandon a abordé en 565 et qu’il a trouvée remplie de choses merveilleuses ». Ce saint Brandon était un saint irlandais, grand voyageur. Les habitants de Madère et de la Gomera prétendaient qu’ils voyaient l’île tous les ans à l’ouest sous la forme d’un nuage et dès avant 1492 elle avait fixé l’attention de Colomb en quête d’arguments pour son premier voyage ; car avant la découverte de l’Amérique, les Canariens regardaient les fruits et les graines d’arbres indigènes aux Antilles, qui s’échouaient sur leurs côtes, comme provenant de l’île Saint-Brandon. L’historien des Canaries, Viera, a donné de forts longs détails sur les tentatives faites de 1487 à 1789 pour y aborder. Elle figure bien entendu sur la mappemonde d’Ortelius de 1583. Elle accompagne sur les cartes ces autres îles imaginaires qui ont nom Antilia et Brazil, dont la dernière n’a pas encore disparu des cartes presque modernes du major Purdy. Au XVIe siècle elle fut cédée, en bonne forme, par les Portugais à un Louis Perdigon qui se préparait à en faire la conquête. Enfin en 1725, dans le recueil de Constantin, on lit ce qui suit la concernant : « A la droite (ouest) des îles Canaries, environ à 100 lieues de distance, on découvre souvent une île qu’on nomme Saint-Borodon. On dit que c’est un lieu couvert de verdure (toujours évidemment) et fort agréable. Les Espagnols ne l’ont jamais pu trouver ; ce qui a fait croire que c’est une illusion ou qu’on n’en peut avoir la vue que certains jours ... ou qu’elle est petite et presque toujours couverte de nuages ... ou que c’est la force des courants qui en sont proches qui fait dériver les vaisseaux et qui les en éloigne. »

 
Il fallait parler de ces îles imaginaires car elles ont joué un rôle dans la navigation  ; elles ont symbolisé le mystère et le secret de la mer, son attrait aussi ; elles ont été comme l’équivalent moderne des sirènes odysséennes ; enfin elles ont entretenu des espérances dans les dures navigations d’autrefois. Et leur rôle n’est pas terminé. II y a quelques années Shakleton se préparait à courir les océans du sud à la recherche de ces autres îles, sans doute imaginaires, qui ont nom Emeraude, Nimrod, Dougherty et qui figurent encore aujourd’hui sur quelques-unes de nos cartes.

 
C’est dans ce chaos, c’est aux prises avec ces difficultés qu’on naviguait ; et il faut admirer le courage de ces hommes qui risquaient leurs vies sur de pareilles incertitudes. Ils étaient tenus à des précautions qui se traduisaient par des pertes de temps.

• On sondait beaucoup avant les atterrissages : Frézier, en 1712, sonda toute la nuit avant d’atterrir à Sainte-Catherine du Brésil.
• Par brume, on tirait du canon, pour écouter l’écho renvoyé par la terre, comme fit Suffren le 22 décembre 1783 pour atterrir à Table bay.
• La nuit, dans des parages trop mal connus, ou quand on était tout à fait dérouté, on faisait petites voiles ou on mettait en panne pour attendre le jour.
  • Ainsi fit Frézier encore, poursuivant sa route vers le sud pour atteindre la terre de Feu et le détroit de Maire. Il y perdit deux nuits.
  • Le procédé classique pour atterrir après une longue traversée consistait à se mettre sur le parallèle du lieu où on voulait reconnaître la terre – car on pouvait avoir des latitudes à peu près exactes – à une distance plus grande que l’erreur estimée sur la longitude, et au vent ; puis on marchait par la même latitude jusqu’à l’atterrissage. Mais cela aussi allongeait la route. De plus, quand la latitude de la carte était erronée, on était sujet à des méprises.
• Les pertes de temps pouvaient devenir alors considérables, et on souffrait à la mer, à ces époques.
  • D’Après, en 1752, s’aperçoit que la latitude de la partie sud de l’Ile de France est erronée et qu’il faut réduire son étendue de 3/7, « ce qu’on ignorait depuis trente ans que nous habitions cette île », dit-il. Cette erreur expliquait que des bâtiments aient manqué l’île, la nuit, et se soient trouvés à l’ouest et sous le vent, le jour suivant. Il leur fallait alors revenir sur leurs pas ; mais les vents étaient debout. Or si on mettait 24 heures pour aller de l’Ile de France à l’île Bourbon, on employait jusqu’à trois semaines pour faire la route inverse, parce qu’il était nécessaire, dans ce cas, de descendre dans le sud pour s’élever au vent en profitant des brises variables qui soufflent sous la zone des alisés. Il fallait faire à peu près la même chose quand on avait manqué l’Ile de France.
  • D’après Rochon, jusqu’en 1775, la latitude de Safi, sur la côte du Maroc, était de même erronée, de sorte que des bâtiments à destination de Safi allaient quelquefois, par erreur, atterrir à Mogador à 1° plus au sud. Ce n’était pas loin ; mais l’alisé de N. E. était juste opposé à la route du retour et il fallait 5 à 6 jours pour rallier Safi. Rochon rectifia cette latitude. On se trompait aussi sur l’estimation de l’erreur en longitude ; on se croyait par exemple à l’est, alors qu’on était à l’ouest ou vice versa. Tels furent, en 1750, d’Après et La Caille, sur le Glorieux vers les îles du Cap-Vert. De même ils n’avaient pas trouvé Madère. Cette île était d’ailleurs difficile à apercevoir. En novembre 1761 le Deptford quitte Portsmouth pour un voyage célèbre, à destination de la Jamaïque. II avait à son bord Littleton, gouverneur de cette colonie. Un autre bâtiment, le Beaver, était parti 10 jours avant lui afin d’arriver à Madère à temps pour y annoncer le passage de Littleton. Mais le Beaver se croyait à l’est de Madère alors qu’il en était en réalité à l’ouest : il fit donc route à l’ouest, à la latitude de Madère, prenant ainsi le large ; et il s’aperçut de son erreur assez tard pour n’arriver à Funchal que trois jours après le Deptford. Cette erreur était si commune, dit la relation du voyage, que des vaisseaux marchands qui marchaient de conserve avec le Deptford avaient fait plusieurs fois le voyage sans jamais apercevoir le petit archipel.
  • Quand les navires se trompaient grossièrement sur la latitude, ne l’observaient pas ou ne pouvaient tomber sur celle qu’ils cherchaient, il pouvait en résulter des inconvénients graves. Or les erreurs sur la latitude étaient fréquentes, contrairement à ce qu’on pourrait croire. Ajoutons quelques nouveaux exemples à ceux déjà donnés. En 1600 le Hollandais Spilberg commet 3° d’erreur sur latitude de Madère, en 1614 il se trompe de 1°5 sur celle des îles du Cap Vert. Vers la même époque ses compatriotes ne savent pas si l’île du Prince est par 1°5 ou 3° de latitude nord.
  • Le Glorieux porté par les vents au nord du Cap, à l’atterrissage sur ce point, mit 20 jours, du 30 mars au 19 avril, pour atteindre Table bay cause « des vents contraires et de leur peu de connaissance de la cote », dit La Caille ; comme Veroheven, en 1607, avait mis 25 jours à faire les 120 milles qui séparent la baie Sainte-Hélène au nord de Table bay du cap de Bonne-Espérance. Mais le cas suivant est encore plus typique. La Sainte-Anne avait quitté l’escadre de Suffren le 16 avril 1781, jour du combat de La Praya. Elle fit route toute seule pour le Cap, dont elle se trouvait à 50 lieues à l’ouest, à l’atterrage le 20 juin. Mais, croyant l’avoir dépassé dans l’est, elle remonta dans le nord. Elle fit donc route au large de la côte occidentale d’Afrique et elle ne reconnut la terre que par 26° de latitude sud, à la Grande-Pequeña. C’était 9° au nord du Cap. Ils n’avaient pas été longs à franchir ; mais pour redescendre dans le sud, il fallut lutter contre des vents debout ; les mêmes qui avaient tant fatigué les Portugais du XVe siècle. Aussi n’arriva-t-elle que le 2 août, 42 jours après Suffren, « ayant perdu, par suite de cette erreur inouïe, la moitié de son équipage ».
  • Dans la relation manuscrite de son voyage à Rodrigue, où il se rendait pour observer le passage de Vénus de 1761, Pingré raconte que son bâtiment a failli périr à l’aller sur les îles du Cap Vert, par suite des erreurs des cartes. En effet, ils étaient passés, de nuit, sans s’en douter, à toucher Boa Vista : ce qui fit dire à un plaisant du bord que « ce n’était pas sans fondement qu’on lui avait dépeint leur vaisseau comme excellent, puisqu’il fendait les terres et les rochers avec autant de facilité que les ondes de l’océan ». L’année suivante, en 1762, le Dromadaire, moins heureux, fit naufrage sur l’île Saint-Vincent du Cap-Vert, par suite d’une erreur des cartes en latitude et, dit d’Après, parce que sa route était mal dirigée.
  • Chappe, dans son mémoire de 1764, cite un ouvrage anglais sur la longitude où il est dit que « depuis 21 ans, plusieurs vaisseaux ont péri par suite de méprises sur la longitude ». Tels sont « le Littchfield, le Ramillies, le Humber, le Dodington, etc. »
  • Nous terminerons par le naufrage de l’Union. Ce bâtiment était parti le 1er novembre 1775 de Ritzembutel (Cuxhaven) pour Gibraltar. Le 14, le vaisseau faisant beaucoup d’eau fut abandonné par la majeure partie de l’équipage. Ceux qui restaient s’estimaient à 40 ou 50 milles du cap Finisterre. Ils finirent pourtant par s’échouer, le 15, sur un banc de sable de la côte de l’île de Ré. On y entretenait déjà, dit la relation, à l’extrémité la plus occidentale, sur une haute tour, appelée la Tour des Baleines, un feu considérable, avec de l’huile.

On comprend maintenant que des efforts aient été faits pour améliorer cet état de choses. Ces difficultés, ces dangers, ces naufrages, retardaient la marche des relations des hommes et le commerce du monde ; et trop de vies et d’argent y étaient intéressés. D’ailleurs, on ne pouvait compter sur les pilotes. Ils étaient pour la plupart ignorants et incapables. Les preuves de leur ignorance abondent. Colomb déjà avait contre eux de véritables accès de rage : « Qu’ils me répondent où est située cette côte de la Veragua où je les ai conduits ? écrivait-il, ils ne sauraient retrouver la route pour y retourner. » Et Vespuce n’est pas moins affirmatif : « L’ignorance de ceux qui gouvernent un navire allonge la route outre mesure. Après cette tempête, il n’y avait aucun de nos pilotes qui sût où nous nous trouvions. Nous allions errants, si par l’astrolabe et le quart de cercle je n’avais pourvu à notre salut. » Au temps de Cortes, dit Navarette, les pilotes savaient à peine lire et éprouvaient de la répugnance à apprendre leur profession. Au commencement du XVIIe siècle ils restaient plongés dans leur ignorance, s’obstinant à ne pas apprendre les éléments scientifiques et à persister dans la routine de leurs devanciers. En 1633 Pedro Porter de Casanate s’élevait contre les abus existants dans l’examen des pilotes et contre la manière dont ils remplissaient leurs devoirs et il attribuait leurs fautes à leur peu d’instruction, à l’imperfection de leurs instruments et l’inexactitude des règles qu’ils suivaient. Enfin ils faisaient des mystères pour cacher leur ignorance, et, par des opérations arbitraires, ils ajoutaient des erreurs nouvelles aux erreurs inhérentes à leurs procédés.

• Radouay a connu un vieux pilote qui se refusait à admettre une erreur dans la distance de Brest au Grand-Banc. « Il demeurait ferme dans son opinion, comme jadis les vieux médecins contre la circulation. » Pour ne pas être obligé d’avouer son erreur, il fit une traversée avec une ampoulette de 24 secondes et il reculait encore son estime de 1/8 sous prétexte que la lame de l’ouest le reculait d’autant. Mais Radouay découvrit la fraude. Il fît tant, du reste, que le vaisseau se trouvait sur le Grand-Banc alors qu’il s’en croyait encore à 50 lieues.
• Bouguer raconte d’un autre qu’il ne pouvait se servir correctement du quartier de réduction. Pour trouver le changement en longitude, il se trompait d’échelle. Pendant longtemps ce pilote fit les traversées Europe-Amérique par la route du nord. Comme cette route le maintenait par des latitudes voisines de 45°, son procédé n’avait pas grand inconvénient ; mais une fois il alla aux Antilles et il allait commettre des erreurs énormes sans les avertissements de gens plus éclairés qui s’aperçurent de son incapacité.
• Quelquefois ils corrigeaient leurs points après l’atterrissage, pour donner à leurs résultats l’apparence de l’exactitude. On lit dans une relation hollandaise d’un voyage dans le Pacifique par l’ouest en 1623 : « Quand les pilotes naviguent au large et que cependant ils ont soupçon d’être près de terre, ils mettent dans leurs cartes le double du chemin qu’ils on fait. » Des procédés analogues expliquent le changement en longitude de 7°6 au lieu de 2°5 qui correspondent à la route ordinaire qu’on trouve dans le journal de Suffren entre le 24 et 15 juin 1781, changement qu’on est tenté d’abord de ne compter que de 3°, parce que les pilotes ont fait traverser le méridien de Paris à la flotte dans cette journée, en ayant soin de ne pas faire suivre les longitudes des lettres W et E. La première est simplement donnée de 5°19’ la deuxième de 2°19’. Le subterfuge est grossier.
• Une négligence de plus, et le naufrage était l’aboutissement de toutes ces méprises. Le P. Tachard, un des Jésuites des ambassades au Siam, raconte celui d’ambassadeurs siamois destinés au Portugal, sur la côte sud d’Afrique. Ils étaient partis de Goa le 27 janvier 1686 sur un vaisseau portugais, de 150 hommes et 30 pièces de canon. La traversée fut qualifiée d’heureuse jusqu’au 27 avril. On avait alors la terre en vue depuis trois jours et on pensa apercevoir le cap de Bonne-Espérance. Jugeant qu’il était dépassé, ou porta donc la route au nord, deux ou trois heures après le coucher du Soleil. On veillait mal ; tout à coup on aperçut sur la droite une ombre épaisse et peu éloignée et aussitôt le navire s’échoua. Bientôt il fut disloqué sur les brisants, car les vents le poussaient à terre. Ils étaient si éloignés du Cap que les survivants mirent 31 jours pour y parvenir à pied le long de la côte.
• En 1700, un grand navire de la Compagnie anglaise des Indes Orientales et un autre, venant de Boston, font naufrage près de l’île Mayotte, qu’ils ont prise pour celle de Moali et il y a entre elles une distance en latitude de 30’ et une différence de longitude de 1°5.
• Radouay et Chabert attribuent la plupart des naufrages à « la fausseté des cartes sur les positions en longitude des terres, îlots, vigies » ; celui de la flûte le Chameau fut dû, d’après le premier, à ce que sur les anciennes cartes la distance du Grand-Banc au cap Breton était portée trop grande de 20 lieues.
• En 1755, le Dodington, au service de la Compagnie anglaise des Indes Orientales, part de la rade des Dunes. Après avoir doublé le cap de Bonne-Espérance et les Agulhas, il fait route à l’est pendant 24 heures, par une latitude sud de 35°5 ; puis il remonte à l’E. N. E. Une vingtaine de jours après il se perdit « sur une petite île formée d’un rocher stérile et inhabité à 33°43’ de latitude sud et à environ 250 lieues du Cap » Il est d’ailleurs impossible de situer exactement le lieu du naufrage, causé par une grosse erreur de navigation. Les survivants, quelques mois après, finirent par arriver à la rivière Sainte-Lucie.

 
Une dernière remarque sur ces résultats et ces procédés. On voit écrire que les portulans étaient d’une extraordinaire précision et qu’ils prouvent la science des pilotes. C’est presque un lieu commun chez certains historiens ou géographes. Après tout ce que nous venons de relever on se demandera comment on peut soutenir une telle assertion. Sans doute, dans ces vieilles cartes la figure des continents est reconnaissable ; mais c’est à peu près tout et si on entre dans le détail des vérifications on constate qu’elles sont grossières et que leur précision est bien au-dessous de celle qui était nécessaire aux navigateurs. On sait combien à la fin du XVIIe siècle encore, la carte de France était incorrecte. Celle de Samson, de 1679 mettait les côtes, depuis l’extrémité de la Bretagne jusqu’à Bayonne, jusqu’à près de 100 kilomètres trop à l’ouest en certaines régions et les côtes de la Méditerranée étaient à peine mieux placées. On sait enfin que la construction d’une carte exacte demande des connaissances théoriques et techniques, des instruments et un travail entièrement et de très loin hors de la portée des pilotes de tous les temps.

 
Ce n’était pas ainsi qu’on pouvait aboutir. Même avec un calcul correct, l’estime, viciée dans ses éléments, ne pouvait conduire au résultat cherché. Les travaux qui s’échelonnent de Nunes à Halley et Cotes pour triompher du problème loxodromique n’avaient eu qu’un effet : celui de classer l’art de la navigation dans les sciences mathématiques ; ce qui était impossible avant Wright, remarquait Herigone, alors qu’une aveugle pratique « cœca praxis » était celle de presque tous les navigateurs. Il fallait travailler et d’abord en dehors des sphères maritimes proprement dites. II fallait avancer l’astronomie, et cette science se trouva ainsi déterminée à progresser sous une impulsion d’ordre essentiellement pratique : le besoin de trouver une solution au problème de la longitude . Or c’est son développement qui fixa presque à lui seul, au XVIIIe siècle au moins, la forme de l’esprit scientifique.